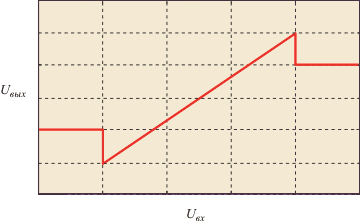
5.4. Особенности реальных регуляторов
Описанный выше ПИД-регулятор и его модификации являются теоретическими идеализациями реальных регуляторов, поэтому для их практического воплощения необходимо учесть особенности, порождаемые реальными условиями применения и технической реализации. К таким особенностям относятся:
- конечный динамический диапазон изменений физических переменных в системе (например, ограниченная мощность нагревателя, ограниченная пропускная способность клапана);
- отсутствие (как правило) в системе поддержания температуры холодильника (управляющее воздействие
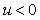 соответствует включению холодильника, а не выключению нагревателя); соответствует включению холодильника, а не выключению нагревателя);
- ограниченная точность измерений, что требует специальных мер для выполнения операций дифференцирования с приемлемой погрешностью;
- наличие практически во всех системах типовых нелинейностей: насыщение (ограничение динамического диапазона изменения переменных), ограничение скорости нарастания, гистерезис и люфт;
- технологический разброс и случайные вариации параметров регулятора и объекта;
- дискретная реализация регулятора;
- необходимость плавного (безударного) переключение режимов регулирования.
Ниже описываются методы решения перечисленных проблем.
5.4.1. Погрешность дифференцирования и шум
Проблема численного дифференцирования является достаточно старой и общей как в цифровых, так и в аналоговых регуляторах. Суть ее заключается в том, что производная вычисляется обычно как разность двух близких по величине значений функции, поэтому относительная погрешность производной всегда оказывается больше, чем относительная погрешность численного представления дифференцируемой функции.
В частности, если на вход дифференциатора поступает синусоидальный сигнал 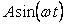 , то на выходе получим , то на выходе получим 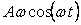 , т.е. с ростом частоты , т.е. с ростом частоты 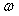 увеличивается амплитуда сигнала на выходе дифференциатора. Иначе говоря, дифференциатор усиливает высокочастотные помехи, короткие выбросы и шум. увеличивается амплитуда сигнала на выходе дифференциатора. Иначе говоря, дифференциатор усиливает высокочастотные помехи, короткие выбросы и шум.
|
|
|
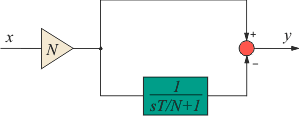
Рис. 5.66. Структурная реализация дифференциального члена ПИД-регулятора
|
Если помехи, усиленные дифференциатором, лежат за границей рабочих частот ПИД-регулятора, то их можно ослабить с помощью фильтра верхних частот. Структурная реализация дифференциатора с фильтром показана на рис. 5.66. Здесь 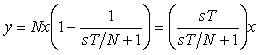 , ,
т.е. передаточная функция полученного дифференциатора 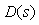 может быть представлена в виде произведения передаточной функции идеального дифференциатора на передаточную функцию фильтра первого порядка: может быть представлена в виде произведения передаточной функции идеального дифференциатора на передаточную функцию фильтра первого порядка: 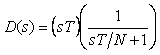 , где коэффициент , где коэффициент 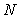 задает граничную частоту фильтра и обычно выбирается равным 2...20 [Astrom]. задает граничную частоту фильтра и обычно выбирается равным 2...20 [Astrom].
Большее ослабление высокочастотных шумов можно получить с помощью отдельного фильтра, который включается последовательно с ПИД-регулятором. Обычно используют фильтр второго порядка [Astrom] с передаточной функцией 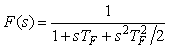 . .
Постоянную времени фильтра обычно выбирают равной 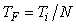 , где , где 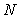 =2...20 [Astrom]. Граничную частоту фильтра желательно не выбирать ниже частоты =2...20 [Astrom]. Граничную частоту фильтра желательно не выбирать ниже частоты 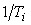 , т.к. это усложняет расчет параметров регулятора и запаса устойчивости. , т.к. это усложняет расчет параметров регулятора и запаса устойчивости.
Кроме шумов дифференцирования на характеристики ПИД-регулятора влияют шумы измерений. Через цепь обратной связи эти шумы поступают на вход системы и затем проявляются как дисперсия управляющей переменной 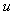 . Высокочастотные шумы вредны тем, что вызывают ускоренный износ трубопроводной арматуры и электродвигателей. . Высокочастотные шумы вредны тем, что вызывают ускоренный износ трубопроводной арматуры и электродвигателей.
Поскольку объект управления обычно является низкочастотным фильтром, шумы измерений редко проникают по контуру регулирования на выход системы. Однако они увеличивают погрешность измерений 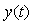 и снижают точность регулирования. и снижают точность регулирования.
В ПИД регуляторах различают шум с низкочастотным спектром, вызванный внешними воздействиями на объект управления, и высокочастотный шум, связанный с электромагнитными наводками, помехами по шинам питания и земли, с дискретизацией измеряемого сигнала и другими причинами [Денисенко, Денисенко]. Низкочастотный шум моделируют как внешние возмущения (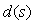 ), высокочастотный - как шумы измерений ( ), высокочастотный - как шумы измерений (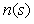 ). ).
5.4.2. Интегральное насыщение
|
|
|
|
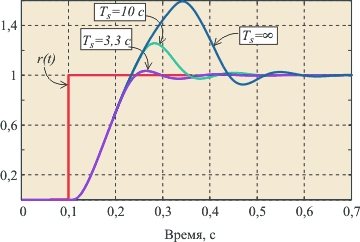
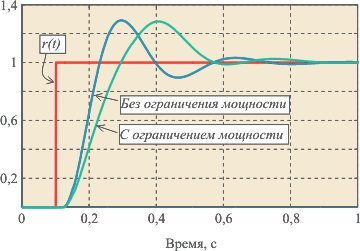
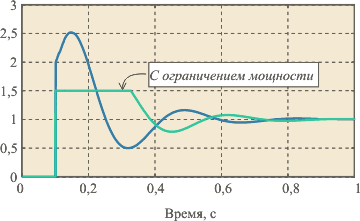
Рис. 5.67. Реакция выходной переменной 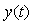 на скачок входного воздействия на скачок входного воздействия 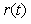 для ПИ-регулятора при условии ограничения мощности на входе объекта для ПИ-регулятора при условии ограничения мощности на входе объекта 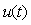 и без ограничения. Объект - второго порядка, и без ограничения. Объект - второго порядка, 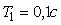 , , 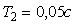 , , 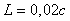 . Параметры регулятора: . Параметры регулятора: 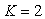 , , 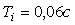 , , 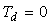 . .
|
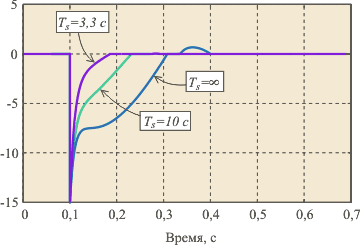
Рис. 5.68. Сигнал на входе объекта 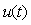 при условии ограничения мощности и без. Объект - второго порядка, при условии ограничения мощности и без. Объект - второго порядка, 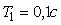 , , 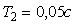 , , 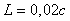 . Параметры регулятора: . Параметры регулятора: 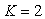 , , 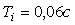 , , 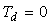 . .
|
В установившемся режиме работы и при малых возмущениях большинство систем с ПИД-регуляторами являются линейными. Однако процесс выхода на режим практически всегда требует учета нелинейности типа "ограничение". Эта нелинейность связана с естественными ограничениями на мощность, скорость, частоту вращения, угол поворота, площадь поперечного сечения клапана, динамический диапазон, и т. п. Контур регулирования в системе, находящейся в насыщении (когда переменная достигла ограничения), оказывается разомкнутым, поскольку при изменении переменной на входе звена с ограничением его выходная переменная остается без изменений.
Наиболее типовым проявлением режима ограничения является так называемое "интегральное насыщение", которое возникает в процессе выхода системы на режим в регуляторах с ненулевой постоянной интегрирования 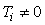 . Интегральное насыщение приводит к затягиванию переходного процесса (рис. 5.67 - рис. 5.68). Аналогичный эффект возникает вследствие ограничения пропорционального и интегрального члена ПИД-регулятора (рис. 5.69 - рис. 5.70). Однако часто под интегральным насыщением понимают совокупность эффектов, связанных с нелинейностью типа "ограничение". . Интегральное насыщение приводит к затягиванию переходного процесса (рис. 5.67 - рис. 5.68). Аналогичный эффект возникает вследствие ограничения пропорционального и интегрального члена ПИД-регулятора (рис. 5.69 - рис. 5.70). Однако часто под интегральным насыщением понимают совокупность эффектов, связанных с нелинейностью типа "ограничение".
Суть проблемы интегрального насыщения состоит в том, что если сигнал на входе объекта управления 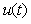 вошел в зону насыщения (ограничения), а сигнал рассогласования вошел в зону насыщения (ограничения), а сигнал рассогласования 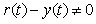 не равен нулю, интегратор продолжает интегрировать т. е. сигнал на его выходе растет, но этот сигнал не участвует в процессе регулирования и не воздействует на объект вследствие эффекта насыщения. Система управления в этом случае становится эквивалентной разомкнутой системе, сигнал на входе которой равен уровню насыщения управляющего сигнала не равен нулю, интегратор продолжает интегрировать т. е. сигнал на его выходе растет, но этот сигнал не участвует в процессе регулирования и не воздействует на объект вследствие эффекта насыщения. Система управления в этом случае становится эквивалентной разомкнутой системе, сигнал на входе которой равен уровню насыщения управляющего сигнала 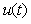 . .
Для тепловых систем ограничением снизу обычно является нулевая мощность нагрева, в то время как ПИД-регулятор требует подачи на объект "отрицательной мощности нагрева", т.е. требует охлаждения объекта.
|
|

|
|
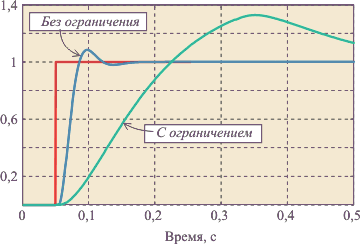
Рис. 5.69. Реакция выходной переменной 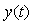 на скачок входного воздействия на скачок входного воздействия 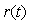 для ПИД-регулятора при условии ограничения мощности на входе объекта для ПИД-регулятора при условии ограничения мощности на входе объекта 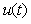 и без ограничения. Объект - второго порядка, и без ограничения. Объект - второго порядка, 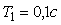 , , 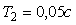 , , 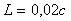 . Параметры регулятора: . Параметры регулятора: 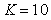 , , 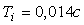 , , 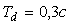 . .
|
Рис. 5.70. Сигнал на входе объекта 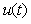 в контуре с ПИД-регулятором при условии ограничения мощности и без. Объект - второго порядка, в контуре с ПИД-регулятором при условии ограничения мощности и без. Объект - второго порядка, 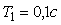 , , 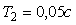 , , 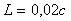 . Параметры регулятора: . Параметры регулятора: 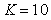 , , 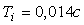 , , 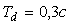 . .
|
Эффект интегрального насыщения известен давно. В аналоговых регуляторах его устранение было достаточно проблематичным, поскольку в них проблема не могла быть решена алгоритмически, а только аппаратными средствами. С появлением микропроцессоров проблему удается решить гораздо эффективнее. Методы устранения интегрального насыщения обычно являются предметом изобретений, относятся к коммерческой тайне фирм-производителей и защищаются патентами. Ниже рассмотрены несколько таких идей, описанных в литературе [Astrom].
Ограничение скорости нарастания входного воздействия
Поскольку максимальное значение входного воздействия на объект управления 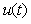 снижается с уменьшением разности снижается с уменьшением разности 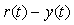 , то для устранения эффекта ограничения можно просто снизить скорость нарастания сигнала уставки , то для устранения эффекта ограничения можно просто снизить скорость нарастания сигнала уставки 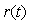 , например, с помощью фильтра. Недостатком такого способа является снижение быстродействия системы, а также невозможность устранить интегральное насыщение, вызванное внешними возмущениями, а не сигналом уставки. , например, с помощью фильтра. Недостатком такого способа является снижение быстродействия системы, а также невозможность устранить интегральное насыщение, вызванное внешними возмущениями, а не сигналом уставки.
Алгоритмический запрет интегрирования
Когда управляющее воздействие на объект достигает насыщения, обратная связь разрывается и интегральная составляющая продолжает расти, даже если при отсутствии насыщения она должна была бы падать. Поэтому один из методов устранения интегрального насыщения состоит в том, что контроллер следит за величиной управляющего воздействия на объект, и как только оно достигает насыщения, контроллер вводит программный запрет интегрирования для интегральной составляющей.
|
|
|
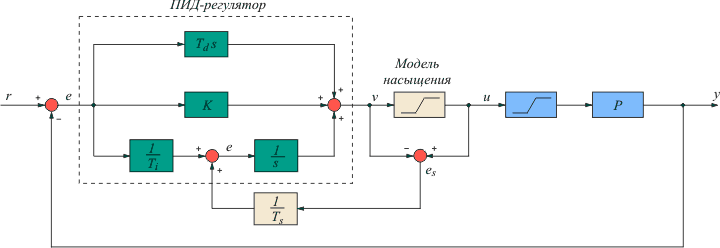
Рис. 5.71. Компенсация эффекта интегрального насыщения с помощью дополнительной обратной связи для передачи сигнала ошибки 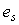 на вход интегратора на вход интегратора
|
Компенсация насыщения с помощью дополнительной обратной связи
Эффект интегрального насыщения можно ослабить, отслеживая состояние исполнительного устройства, входящего в насыщение, и компенсируя сигнал, подаваемый на вход интегратора [Astrom]. Структура системы с таким компенсатором показана на рис. 5.71.
Принцип ее работы состоит в следующем. В системе вырабатывается сигнал рассогласования между входом и выходом исполнительного устройства 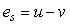 . Сигнал на выходе исполнительного устройства либо измеряют, либо вычисляют, используя математическую модель (рис. 5.71). Если . Сигнал на выходе исполнительного устройства либо измеряют, либо вычисляют, используя математическую модель (рис. 5.71). Если 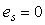 , это эквивалентно отсутствию компенсатора и получаем обычный ПИД-регулятор. Если же исполнительное устройство входит в насыщение, то , это эквивалентно отсутствию компенсатора и получаем обычный ПИД-регулятор. Если же исполнительное устройство входит в насыщение, то 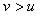 и и 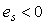 . При этом сигнал на входе интегратора уменьшается на величину ошибки . При этом сигнал на входе интегратора уменьшается на величину ошибки 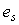 , что приводит к замедлению роста сигнала на выходе интегратора, уменьшению сигнала рассогласования и величины выброса на переходной характеристике системы (рис. 5.72). Постоянная времени , что приводит к замедлению роста сигнала на выходе интегратора, уменьшению сигнала рассогласования и величины выброса на переходной характеристике системы (рис. 5.72). Постоянная времени 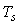 определяет степень компенсации сигнала рассогласования (рис. 5.72). определяет степень компенсации сигнала рассогласования (рис. 5.72).
В некоторых регуляторах вход 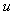 устройства сравнения устройства сравнения 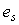 выделяют как отдельный вход, называемый "вход слежения", что бывает удобно при построении сложных систем управления и при каскадном соединении нескольких регуляторов. выделяют как отдельный вход, называемый "вход слежения", что бывает удобно при построении сложных систем управления и при каскадном соединении нескольких регуляторов.
Условное интегрирование
Этот способ является обобщением алгоритмического запрета интегрирования. После наступления запрета интегральная составляющая остается постоянной, на том же уровне, который она имела в момент появления запрета интегрирования. Обобщение состоит в том, что запрет интегрирования наступает не только при достижении насыщения, но и при некоторых других условиях.
Такими условиями могут быть, например, достижение сигналом ошибки 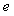 или выходной переменной или выходной переменной 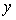 некоторого заданного значения. При выключении процесса интегрирования нужно следить, в каком состоянии в момент выключения находится интегратор. Если он накапливает ошибку и степень насыщения возрастает, то интегрирование выключают. Если же в момент выключения степень насыщения понижается, то интегратор оставляют включенным [Astrom]. некоторого заданного значения. При выключении процесса интегрирования нужно следить, в каком состоянии в момент выключения находится интегратор. Если он накапливает ошибку и степень насыщения возрастает, то интегрирование выключают. Если же в момент выключения степень насыщения понижается, то интегратор оставляют включенным [Astrom].
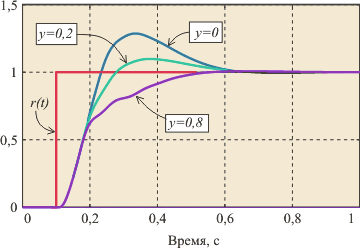
На рис. 5.73 показан пример переходного процесса в системе с отключением интегратора при достижении выходной величины 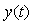 заданного значения ( заданного значения (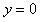 , , 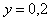 , , 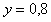 ). ).
Интегратор с ограничением
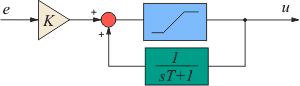
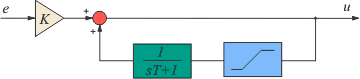
На рис. 5.58 был представлен вариант реализации ПИ-регулятора с помощью интегратора в цепи обратной связи. Если эту схему дополнить ограничителем (рис. 5.74-а), то сигнал 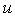 на выходе никогда не выйдет за границы, установленные порогами ограничителя, что уменьшает выброс на переходной характеристике системы (рис. 5.75). На рис. 5.74,б представлена модификация такого ограничителя. на выходе никогда не выйдет за границы, установленные порогами ограничителя, что уменьшает выброс на переходной характеристике системы (рис. 5.75). На рис. 5.74,б представлена модификация такого ограничителя.
Модель эффекта ограничения можно улучшить, если после превышении уровня, при котором наступает ограничение, уменьшить сигнал на выходе модели (рис. 5.76) [Astrom]. Это ускоряет выход системы из режима насыщения.
 |
 |
|
а)
|
б) |
|
Рис. 5.74. Модификации интегратора с ограничением.
|
5.4.3. Запас устойчивости и робастность
Возможность потери устойчивости является основным недостатком систем с обратной связью. Поэтому обеспечение необходимого запаса устойчивости являются самым важным этапом при разработке и настройке ПИД-регулятора.
Устойчивость системы с ПИД-регулятором - это способность системы возвращаться к слежению за уставкой после прекращения действия внешних воздействий. В контексте данного определения под внешними воздействиями понимаются не только внешние возмущения, действующие на объект, но любые возмущения, действующие на любую часть замкнутой системы, в том числе шумы измерений, временная нестабильность уставки, шумы дискретизации и квантования, шумы и погрешность вычислений. Все эти возмущения вызывают отклонения системы от положения равновесия. Если после прекращения воздействия система возвращается в положение равновесия, то она считается устойчивой. При анализе устойчивости ПИД-регуляторов обычно ограничиваются исследованием реакции системы на ступенчатое изменение уставки 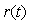 , шум измерений , шум измерений 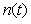 и внешние возмущения и внешние возмущения 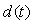 . Потеря устойчивости проявляется как неограниченное возрастание управляемой переменной объекта, или как ее колебание с нарастающей амплитудой. . Потеря устойчивости проявляется как неограниченное возрастание управляемой переменной объекта, или как ее колебание с нарастающей амплитудой.
|
|
|
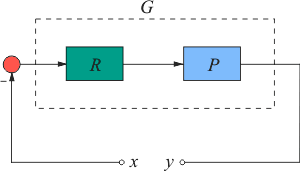
Рис. 5.77. Структура разомкнутой системы управления с ПИД-регулятором для анализа устойчивости
|
В производственных условиях попытки добиться устойчивости системы с ПИД-регулятором опытным путем, без ее идентификации, не всегда приводят к успеху (например, для систем с объектом высокого порядка, для систем с большой транспортной задержкой или для объектов, которые трудно идентифицировать). Это создает впечатление, что устойчивость - мистическое свойство, которым не всегда можно управлять. Однако, если процесс идентифицирован достаточно точно, то мистика исчезает и анализ устойчивости сводится к анализу дифференциального уравнения, описывающего замкнутый контур с обратной связью.
Практически интерес представляет анализ запаса устойчивости, т. е. определение численных значений критериев, которые позволяют указать, как далеко находится система от состояния неустойчивости.
Наиболее полную информацию о запасе устойчивости системы можно получить, решив дифференциальное уравнение, описывающее замкнутую систему при внешних возмущениях. Однако этот процесс слишком трудоемок, поэтому для линейных систем используют упрощенные методы, позволяющие дать оценку запаса устойчивости без решения уравнений [Воронов]. Мы рассмотрим два метода: оценку с помощью годографа комплексной частотной характеристики разомкнутого контура (критерий Найквиста) и с помощью логарифмических АЧХ и ФЧХ (диаграмм Боде).
Устойчивая система может стать неустойчивой при небольших изменениях ее параметров, например, вследствие их технологического разброса. Поэтому ниже мы проанализируем функцию чувствительности системы с ПИД-регулятором, которая позволяет выявить условия, при которых система становится грубой (мало чувствительной к изменению ее параметров).
Система, которая сохраняет заданный запас устойчивости во всем диапазоне изменений параметров вследствие их технологического разброса, старения, условий эксплуатации, во всем диапазоне изменений параметров нагрузки, а также во всем диапазоне действующих на систему возмущений в реальных условиях эксплуатации, называют робастной. Иногда робастность и грубость используют как эквивалентные понятия.
Критерий Найквиста
Рассмотрим систему, состоящую из контроллера 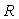 и объекта управления и объекта управления 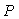 (рис. 5.77), которая получена путем исключения из классической системы с ПИД-регулятором (рис. 5.34) сигнала уставки (рис. 5.77), которая получена путем исключения из классической системы с ПИД-регулятором (рис. 5.34) сигнала уставки 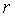 . Будем считать, что обратная связь разомкнута, а для ее замыкания достаточно соединить точки . Будем считать, что обратная связь разомкнута, а для ее замыкания достаточно соединить точки 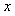 и и 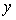 . Предположим теперь, что на вход . Предположим теперь, что на вход 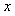 подан сигнал подан сигнал
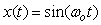 . . |
(5.86)
|
Тогда, пройдя через регулятор и объект управления, этот сигнал появится на выходе 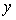 с измененной амплитудой и фазой, в виде с измененной амплитудой и фазой, в виде
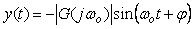 , , |
(5.87)
|
где 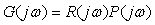 - комплексная частотная характеристика (КЧХ) системы, - комплексная частотная характеристика (КЧХ) системы, 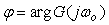 - аргумент КЧХ, - аргумент КЧХ, 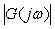 - модуль КЧХ. Таким образом, при прохождении через регулятор и объект амплитуда сигнала изменится пропорционально модулю, а фаза - на величину аргумента КЧХ. - модуль КЧХ. Таким образом, при прохождении через регулятор и объект амплитуда сигнала изменится пропорционально модулю, а фаза - на величину аргумента КЧХ.
Если теперь замкнуть точки 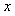 и и 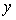 , то сигнал будет циркулировать по замкнутому контуру, причем будет выполняться условие , то сигнал будет циркулировать по замкнутому контуру, причем будет выполняться условие 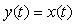 . Если при этом . Если при этом 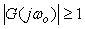 и и 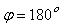 , т.е. после прохождения по контуру сигнал попадает на вход регулятора в той же фазе, что и на предыдущем цикле, то после каждого прохождения по контуру амплитуда синусоидального сигнала будет возрастать, пока не достигнет границы диапазона линейности системы, после чего форма колебаний станет отличаться от синусоидальной. В этом случае для анализа устойчивости можно использовать метод гармонической линеаризации, когда рассматривают только первую гармонику искаженного сигнала. В установившемся режиме после наступления ограничения амплитуды колебаний в силу равенства , т.е. после прохождения по контуру сигнал попадает на вход регулятора в той же фазе, что и на предыдущем цикле, то после каждого прохождения по контуру амплитуда синусоидального сигнала будет возрастать, пока не достигнет границы диапазона линейности системы, после чего форма колебаний станет отличаться от синусоидальной. В этом случае для анализа устойчивости можно использовать метод гармонической линеаризации, когда рассматривают только первую гармонику искаженного сигнала. В установившемся режиме после наступления ограничения амплитуды колебаний в силу равенства 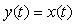 будет выполняться условие будет выполняться условие
Решив уравнение 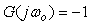 , можно найти частоту колебаний , можно найти частоту колебаний 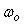 в замкнутой системе. в замкнутой системе.
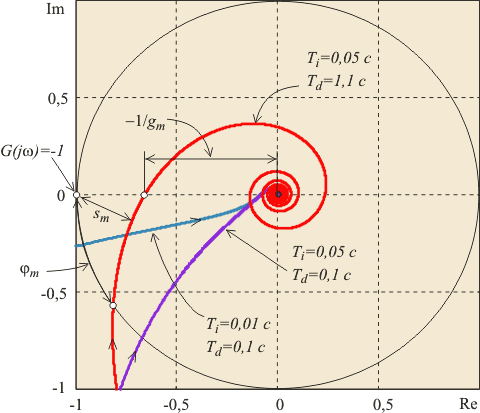
Комплексную частотную характеристику 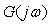 графически изображают в виде годографа (диаграммы Найквиста) - графика в координатах графически изображают в виде годографа (диаграммы Найквиста) - графика в координатах 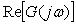 и и 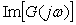 (рис. 5.78). Стрелка на линии годографа указывает направление движения "карандаша" при возрастании частоты. Точка (рис. 5.78). Стрелка на линии годографа указывает направление движения "карандаша" при возрастании частоты. Точка 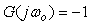 , которая соответствует условию существования незатухающих колебаний в системе, на этом графике имеет координаты , которая соответствует условию существования незатухающих колебаний в системе, на этом графике имеет координаты 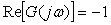 и и 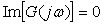 . Поэтому критерий устойчивости Найквиста формулируется следующим образом [Ротач]: контур, устойчивый в разомкнутом состоянии, сохранит устойчивость и после его замыкания, если его КЧХ в разомкнутом состоянии не охватывает точку с координатами [-1, j0]. Более строго, при движении вдоль траектории годографа в направлении увеличения частоты точка [-1, j0] должна оставаться слева [Astrom], чтобы замкнутый контур был устойчив. . Поэтому критерий устойчивости Найквиста формулируется следующим образом [Ротач]: контур, устойчивый в разомкнутом состоянии, сохранит устойчивость и после его замыкания, если его КЧХ в разомкнутом состоянии не охватывает точку с координатами [-1, j0]. Более строго, при движении вдоль траектории годографа в направлении увеличения частоты точка [-1, j0] должна оставаться слева [Astrom], чтобы замкнутый контур был устойчив.
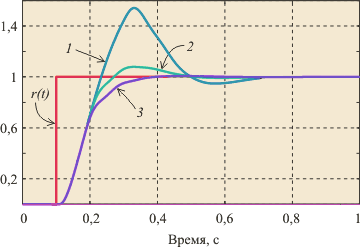
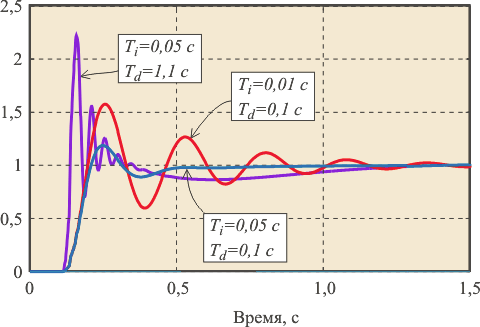
На рис. 5.79 показаны реакции замкнутых систем с тремя различными годографами (рис. 5.78) на единичный скачок уставки. Все три системы устойчивы, однако скорость затухания колебаний и форма переходного процесса у них различная. Интуитивно понятно, что система с параметрами 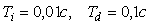 наиболее близка к тому, чтобы перейти в состояние незатухающих колебаний при небольшом изменении ее параметров. Поэтому при проектировании ПИД-регулятора важно обеспечить не столько устойчивость, сколько ее запас, необходимый для нормального функционирования системы в реальных условиях. наиболее близка к тому, чтобы перейти в состояние незатухающих колебаний при небольшом изменении ее параметров. Поэтому при проектировании ПИД-регулятора важно обеспечить не столько устойчивость, сколько ее запас, необходимый для нормального функционирования системы в реальных условиях.
Запас устойчивости оценивают как степень удаленности КЧХ от критической точки [-1, j0]. Если 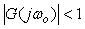 , то можно найти, во сколько раз осталось увеличить передаточную функцию, чтобы результирующее усиление вывело систему в колебательный режим: , то можно найти, во сколько раз осталось увеличить передаточную функцию, чтобы результирующее усиление вывело систему в колебательный режим: 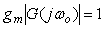 , откуда , откуда
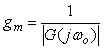 |
(5. 89) |
Запасом по усилению 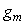 называется величина, на которую нужно умножить передаточную функцию разомкнутой системы называется величина, на которую нужно умножить передаточную функцию разомкнутой системы 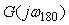 , чтобы ее модуль на частоте сдвига фаз 180˚ , чтобы ее модуль на частоте сдвига фаз 180˚ 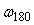 стал равен 1. стал равен 1.
Если на частоте сдвига фаз 180˚ 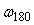 коэффициент усиления разомкнутого контура равен коэффициент усиления разомкнутого контура равен 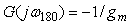 (рис. 5.78), то дополнительное усиление величиной (рис. 5.78), то дополнительное усиление величиной 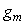 переведет систему в точку [-1, j0], поскольку переведет систему в точку [-1, j0], поскольку 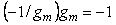 . .
Аналогично вводится понятие запаса по фазе: это минимальная величина 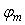 , на которую нужно увеличить фазовый сдвиг в разомкнутой системе , на которую нужно увеличить фазовый сдвиг в разомкнутой системе 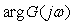 , чтобы суммарный фазовый сдвиг достиг 180˚, т.е. , чтобы суммарный фазовый сдвиг достиг 180˚, т.е.
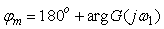 . . |
(5.90)
|
|
|
|
Рис. 5.79. Переходная характеристика замкнутой системы, которая имеет годограф, показанный на рис. 5.78
|
Знак "+" перед 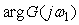 стоит потому, что стоит потому, что 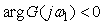 . .
Для оценки запаса устойчивости используют также минимальное расстояние 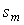 от кривой годографа до точки [-1, j0] (рис. 5.78). от кривой годографа до точки [-1, j0] (рис. 5.78).
На практике считаются приемлемыми значения 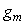 =2...5, =2...5, 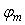 =30˚...60˚, =30˚...60˚, 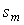 =0,5...0,8 [Astrom]. =0,5...0,8 [Astrom].
Для графика на рис. 5.78 эти критерии имеют следующие значения:
- для случая
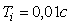 , , 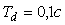 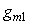 =12,1; =12,1; 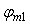 =15˚; =15˚; 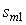 =0,303. =0,303.
- для случая
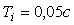 , , 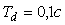 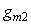 =11,8; =11,8; 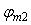 =47,6; =47,6; 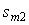 =0,663. =0,663.
- для случая
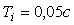 , , 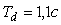 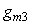 =1,5; =1,5; 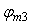 =35,2; =35,2;  =0,251. =0,251.
Если кривая годографа пересекает действительную ось в нескольких точках, то для оценки запаса устойчивости берут ту из них, которая наиболее близка к точке [-1, j0]. При более сложном годографе может быть использована оценка запаса устойчивости как запас по задержке [Astrom]. Запас по задержке- это минимальная задержка, при добавлении которой в контур он теряет устойчивость. Наиболее часто этот критерий используется для оценки запаса устойчивости систем с предиктором Смита.
Частотный критерий устойчивости
|
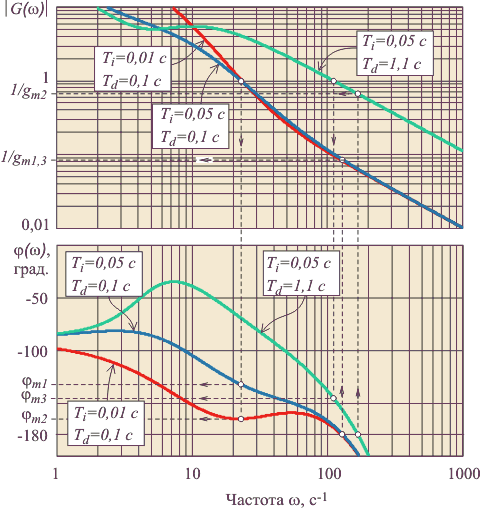
|
|
Рис. 5.80. Оценка запаса по фазе и усилению для системы с годографом, показанным на рис. 5.78
|
Для графического представления передаточной функции разомкнутой системы и оценки запаса устойчивости могут быть использованы логарифмические АЧХ и ФЧХ (рис. 5.80). Для оценки запаса по фазе сначала с помощью АЧХ находят частоту 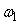 ("частота среза" или "частота единичного усиления"), при которой ("частота среза" или "частота единичного усиления"), при которой 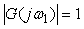 , затем по ФЧХ находят соответствующий запас по фазе. Для оценки запаса по усилению сначала с помощью ФЧХ находят частоту , затем по ФЧХ находят соответствующий запас по фазе. Для оценки запаса по усилению сначала с помощью ФЧХ находят частоту 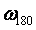 , на которой фазовый сдвиг равен 180˚, затем по АЧХ находят запас по усилению. На (рис. 5.80) приведены примеры графических построений для оценки запаса по фазе и усилению для системы, годограф которой показан на рис. 5.78. , на которой фазовый сдвиг равен 180˚, затем по АЧХ находят запас по усилению. На (рис. 5.80) приведены примеры графических построений для оценки запаса по фазе и усилению для системы, годограф которой показан на рис. 5.78.
Если запас по фазе разомкнутого контура равен 0˚ или запас по усилению равен 1, после замыкания контура обратной связи система окажется неустойчивой.
Функции чувствительности
Передаточная функция реального объекта 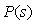 может изменяться в процессе функционирования на величину может изменяться в процессе функционирования на величину 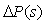 , например, вследствие изменения нагрузки на валу двигателя, числа яиц в инкубаторе, уровня или состава жидкости в автоклаве, вследствие старения и износа материала, появления люфта, изменения смазки и т.п. Правильно спроектированная система автоматического регулирования должна сохранять свои показатели качества не только в идеальных условиях, но и при наличии перечисленных вредных факторов. Для оценки влияния относительного изменения передаточной функции объекта , например, вследствие изменения нагрузки на валу двигателя, числа яиц в инкубаторе, уровня или состава жидкости в автоклаве, вследствие старения и износа материала, появления люфта, изменения смазки и т.п. Правильно спроектированная система автоматического регулирования должна сохранять свои показатели качества не только в идеальных условиях, но и при наличии перечисленных вредных факторов. Для оценки влияния относительного изменения передаточной функции объекта 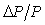 на передаточную функция замкнутой системы на передаточную функция замкнутой системы 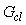 (5.41) найдем дифференциал (5.41) найдем дифференциал 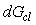 : :
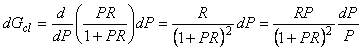 . . |
(5. 91)
|
Поделив обе части этого равенства на 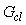 и подставив в правую часть и подставив в правую часть 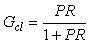 , получим , получим
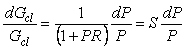 . . |
(5.92)
|
Из последнего соотношения виден смысл коэффициента 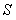 - он характеризует степень влияния относительного изменения передаточной функции объекта на относительное изменение передаточной функции замкнутого контура, то есть - он характеризует степень влияния относительного изменения передаточной функции объекта на относительное изменение передаточной функции замкнутого контура, то есть 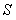 является коэффициентом чувствительности замкнутого контура к вариации передаточной функции объекта. Поскольку коэффициент является коэффициентом чувствительности замкнутого контура к вариации передаточной функции объекта. Поскольку коэффициент 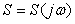 является частотозависимым, его называют функцией чувствительности [Astrom]. является частотозависимым, его называют функцией чувствительности [Astrom].
Как следует из (5.92),
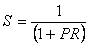 . . |
(5. 93)
|
|
Введем обозначение 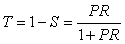 . .
|
(5.94)
|
|
|
|
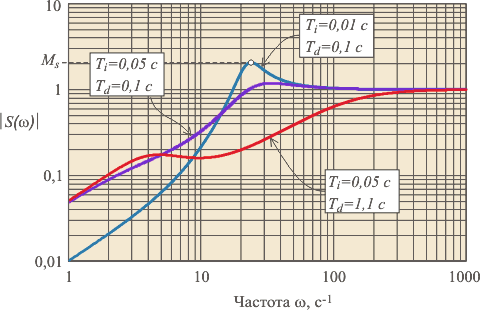
Рис. 5.81. Модули функций чувствительности для систем с годографами, показанными на рис. 5.78
|
Величина  называется комплементарной (дополнительной) функцией чувствительности [Astrom], поскольку называется комплементарной (дополнительной) функцией чувствительности [Astrom], поскольку 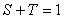 . .
Заметим, что функция чувствительности входит во все три слагаемые уравнения замкнутой системы с ПИД-регулятором (5.42).
Функция чувствительности позволяет оценить изменение свойств системы после замыкания обратной связи. Поскольку передаточная функция разомкнутой системы равна 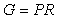 , а замкнутой , а замкнутой 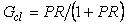 , то их отношение , то их отношение 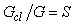 . Аналогично, передаточная функция от входа возмущений . Аналогично, передаточная функция от входа возмущений 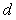 на выход замкнутой системы равна на выход замкнутой системы равна 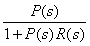 (см. (5.42)), а разомкнутой - (см. (5.42)), а разомкнутой - 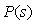 , следовательно, их отношение также равно , следовательно, их отношение также равно 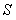 . Для передаточной функции от входа шума измерений . Для передаточной функции от входа шума измерений 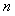 на выход системы можно получить то же отношение на выход системы можно получить то же отношение 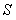 . .
Таким образом, зная вид функции 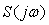 (см, например, рис. 5.81), можно сказать, как изменится подавление внешних воздействий на систему для разных частот после замыкания цепи обратной связи. Очевидно, шумы, лежащие в диапазоне частот, в котором (см, например, рис. 5.81), можно сказать, как изменится подавление внешних воздействий на систему для разных частот после замыкания цепи обратной связи. Очевидно, шумы, лежащие в диапазоне частот, в котором 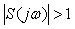 , после замыкания обратной связи будут усиливаться, а шумы с частотами, на которых , после замыкания обратной связи будут усиливаться, а шумы с частотами, на которых 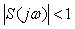 , после замыкания обратной связи будут ослаблены. , после замыкания обратной связи будут ослаблены.
Наихудший случай (наибольшее усиление внешних воздействий) будет наблюдаться на частоте максимума 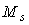 модуля функции чувствительности (рис. 5.81): модуля функции чувствительности (рис. 5.81):
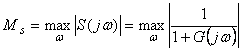 . . |
(5.95)
|
Максимум функции чувствительности можно связать с запасом устойчивости 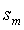 (рис. 5.78). Для этого обратим внимание, что (рис. 5.78). Для этого обратим внимание, что 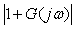 представляет собой расстояние от точки (-1, j0) до текущей точки на годографе функции представляет собой расстояние от точки (-1, j0) до текущей точки на годографе функции 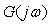 . Следовательно, минимальное расстояние от точки (-1, j0) до функции . Следовательно, минимальное расстояние от точки (-1, j0) до функции 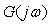 равно равно
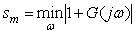 . . |
(5.96)
|
Сопоставляя (5.95) и (5.96), можно заключить, что 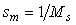 . .
Если с ростом частоты модуль 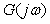 уменьшается, то, как видно из (рис. 5.78), уменьшается, то, как видно из (рис. 5.78), 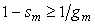 . Подставляя сюда соотношение . Подставляя сюда соотношение 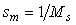 , получим оценку запаса по усилению, выраженную через максимум функции чувствительности: , получим оценку запаса по усилению, выраженную через максимум функции чувствительности:
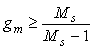 . . |
(5.97)
|
Аналогично, но с более грубыми допущениями можно записать оценку запаса по фазе через максимум функции чувствительности [Astrom]:
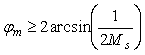 . . |
(5.98)
|
Например, при 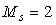 получим получим 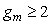 и и 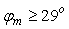 . .
Робастность
Робастность - это способность системы сохранять заданный запас устойчивости при вариациях ее параметров, вызванных изменением нагрузки (например, при изменении загрузки печи меняются ее постоянные времени), технологическим разбросом параметров и их старением, внешними воздействиями, погрешностями вычислений и погрешностью модели объекта. Используя понятие чувствительности, можно сказать, что робастность - это низкая чувствительность запаса устойчивости к вариации параметров объекта.
Если параметры объекта изменяются в небольших пределах, когда можно использовать замену дифференциала конечным приращением, влияние изменений параметров объекта на передаточную функцию замкнутой системы можно оценить с помощью функции чувствительности (5.92). В частности, можно сделать вывод, что на тех частотах, где модуль функции чувствительности мал, будет мало и влияние изменений параметров объекта на передаточную функцию замкнутой системы и, соответственно, на запас устойчивости.
Для оценки влияния больших изменения параметров объекта представим передаточную функцию объекта в виде двух слагаемых
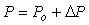 , , |
(5.99)
|
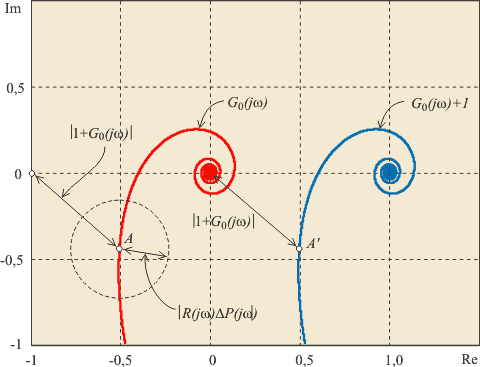
где 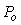 - расчетная передаточная функция, - расчетная передаточная функция, 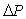 - величина отклонения от - величина отклонения от 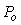 , которая должна быть устойчивой передаточной функцией. Тогда петлевое усиление разомкнутой системы можно представить в виде , которая должна быть устойчивой передаточной функцией. Тогда петлевое усиление разомкнутой системы можно представить в виде 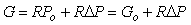 . Поскольку расстояние от точки (-1, j0) до текущей точки . Поскольку расстояние от точки (-1, j0) до текущей точки 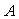 на годографе невозмущенной системы (для которой на годографе невозмущенной системы (для которой 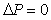 ) равно ) равно 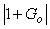 (см. рис. 5.82), условие устойчивости системы с отклонением петлевого усиления (см. рис. 5.82), условие устойчивости системы с отклонением петлевого усиления 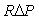 можно представить в виде можно представить в виде
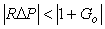 , откуда 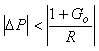 , или , или 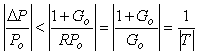 , ,
где  - дополнительная функция чувствительности (5.94). Окончательно можно записать соотношение - дополнительная функция чувствительности (5.94). Окончательно можно записать соотношение
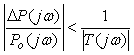 , , |
(5.100)
|
|
|
|
Рис. 5.82. Пояснение к выводу соотношения (5.100)
|
которое должно выполняться, чтобы система сохраняла устойчивость при изменении параметров процесса на величину 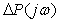 . .
5.4.4. Сокращение нулей и полюсов
Поскольку передаточная функция разомкнутой системы 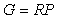 является произведением двух передаточных функций, которые в общем случае имеют и числитель, и знаменатель, то возможно сокращение нулей с полюсами, которые лежат в правой полуплоскости или близки к ней. Поскольку в реальных условиях, когда существует разброс параметров, такое сокращение выполняется неточно, то может возникнуть ситуация, когда теоретический анализ приводит к выводу, что система устойчива, хотя на самом деле при небольшом отклонении параметров процесса от расчетных значений она становится неустойчивой. является произведением двух передаточных функций, которые в общем случае имеют и числитель, и знаменатель, то возможно сокращение нулей с полюсами, которые лежат в правой полуплоскости или близки к ней. Поскольку в реальных условиях, когда существует разброс параметров, такое сокращение выполняется неточно, то может возникнуть ситуация, когда теоретический анализ приводит к выводу, что система устойчива, хотя на самом деле при небольшом отклонении параметров процесса от расчетных значений она становится неустойчивой.
Поэтому каждый раз, когда происходит сокращение нулей и полюсов, необходимо проверять устойчивость системы при реальном разбросе параметров объекта.
Вторым эффектом является появление существенного различия между временем установления переходного процесса при воздействии сигнала уставки и внешних возмущений. Поэтому необходимо проверять реакцию синтезированного регулятора для каждого из этих воздействаий.
5.4.5. Безударное переключение режимов регулирования
В ПИД-регуляторах могут существовать режимы, когда их параметры изменяются скачком. Например, когда в работающей системе потребовалось изменить постоянную интегрирования или если после ручного управления системой необходимо перейти на автоматический режим. В описанных случаях могут появиться нежелательные выбросы регулируемой величины, если не принять специальных мер. Поэтому возникает задача плавного ("безударного") переключения режимов работы или параметров регулятора.
Основной метод решения проблемы заключается в построении такой структуры регулятора, когда изменение параметра выполнятся до этапа интегрирования. Например, при изменяющемся параметре 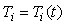 интегральный член можно записать в двух формах: интегральный член можно записать в двух формах:
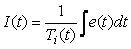 или 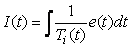 . В первом случае при скачкообразном изменении 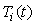 интегральный член будет меняться скачком, во втором случае - плавно, поскольку интегральный член будет меняться скачком, во втором случае - плавно, поскольку 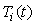 находится под знаком интеграла, значение которого не может изменяться скачком. находится под знаком интеграла, значение которого не может изменяться скачком.
Аналогичный метод реализуется в инкрементной форме ПИД-регулятора (см. раздел "Инкрементная форма цифрового ПИД-регулятора") и в последовательной форме ПИД-регулятора, где интегрирование выполняется на заключительной стадии вычисления управляющего воздействия.
5.4.6. Дискретная форма регулятора
Непрерывные переменные удобно использовать для анализа и синтеза ПИД-регуляторов. Для технического воплощения необходимо перейти к дискретной форме уравнений, поскольку основой всех регуляторов является микроконтроллер, контроллер или компьютер, которые оперируют с переменными, полученными из аналоговых сигналов после их дискретизации по времени и квантования по уровню.
Вследствие конечного времени вычисления управляющего воздействия в микроконтроллере и задержки аналого-цифрового преобразования между моментом поступления аналогового сигнала на вход регулятора и появлением управляющего воздействия на его выходе появляется нежелательная задержка, которая увеличивает общую задержку в контуре регулирования и снижает запас устойчивости.
Основным эффектом, который появляется при дискретизации и который часто "открывают заново", является появление алиасных частот в спектре квантованного сигнала в случае, когда частота дискретизации недостаточно высока. Аналогичный эффект возникает при киносъемке вращающегося колеса автомобиля. Частота алиасного сигнала равна разности между частотой помехи и частотой дискретизации. При этом высокочастотный сигнал помехи смещается в низкочастотную область, где накладывается на полезный сигнал и создает большие проблемы, поскольку отфильтровать его на этой стадии невозможно.
Для устранения алиасного эффекта перед входом аналого-цифрового преобразователя необходимо установить аналоговый фильтр, который бы ослаблял помеху по крайне мере на порядок на частоте, равной половине частоты дискретизации. Обычно используют фильтр Баттерворта второго или более высокого порядка. Вторым вариантом решения проблемы является увеличение частоты дискретизации так, чтобы она по крайней мере в 2 раза (согласно теореме Котельникова) была выше максимальной частоты спектра помехи. Это позволяет применить после дискретизации цифровой фильтр нижних частот. При такой частоте дискретизации полученный цифровой сигнал с точки зрения количества информации полностью эквивалентен аналоговому и все свойства аналогового регулятора можно распространить на цифровой.
Переход к конечно-разностным уравнениям
Переход к дискретным переменным в уравнениях аналогового регулятора выполняется путем замены производных и интегралов их дискретными аналогами. Если уравнение записано в операторной форме, то сначала выполняют переход из области изображений в область оригиналов. При этом оператор дифференцирования заменяют производной, оператор интегрирования - интегралом.
Существует множество способов аппроксимации производных и интегралов их дискретными аналогами, которые изложены в курсах численных методов решения дифференциальных уравнений. В ПИД-регуляторах наиболее распространенными являются простейшая аппроксимация производной конечной разностью и интеграла - конечной суммой.
Рассмотрим интегральный член ПИД-регулятора: 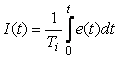 . Продифференцировав обе части по времени, получим . Продифференцировав обе части по времени, получим 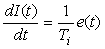 . Заменяя дифференциалы в этом выражении конечными разностями (левыми разностями), получим . Заменяя дифференциалы в этом выражении конечными разностями (левыми разностями), получим 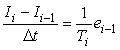 , где индекс , где индекс 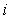 обозначает, что данная величина взята в момент времени обозначает, что данная величина взята в момент времени 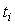 (обратим внимание, что здесь и ниже индекс (обратим внимание, что здесь и ниже индекс 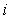 в в  обозначает не номер временного шага, а интегральный коэффициент ПИД-регулятора). Из последнего выражения получим обозначает не номер временного шага, а интегральный коэффициент ПИД-регулятора). Из последнего выражения получим
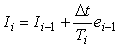 . . |
(5.101)
|
Таким образом, очередное значение интеграла можно вычислить, зная предыдущее и значение ошибки в предыдущий момент времени. Однако такая формула имеет свойство накапливать ошибку вычислений с течением времени, если отношение 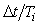 недостаточно мало. Более устойчива другая формула интегрирования с правыми разностями, когда значение ошибки берется в тот же момент времени, что и вычисляемый интеграл: недостаточно мало. Более устойчива другая формула интегрирования с правыми разностями, когда значение ошибки берется в тот же момент времени, что и вычисляемый интеграл:
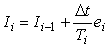 . . |
(5.102)
|
Рассмотрим дифференциальный член ПИД-регулятора с фильтром 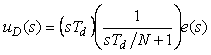 (см. раздел "Погрешность дифференцирования и шум"). (см. раздел "Погрешность дифференцирования и шум").
Переходя в этой формуле от изображений к оригиналам, получим 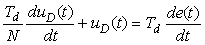 . Заменяя дифференциалы конечными приращениями, получим разностное уравнение . Заменяя дифференциалы конечными приращениями, получим разностное уравнение
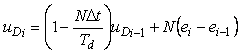 . . |
(5.103)
|
Для сходимости итерационного процесса (5.103) необходимо, чтобы 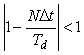 , т.е. , т.е.
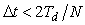 . . |
(5.104)
|
При 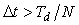 итерационный процесс (5.103) становится колебательным, что недопустимо для ПИД-регулятора. итерационный процесс (5.103) становится колебательным, что недопустимо для ПИД-регулятора.
Лучшими характеристиками обладает разностное уравнение, полученное при использовании правых разностей:
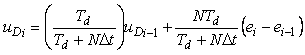 . . |
(5.105)
|
Здесь условие сходимости 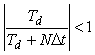 выполняется для всех выполняется для всех 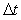 и ни при каких значениях параметров не возникает колебаний. Кроме того, последняя формула позволяет "отключить" дифференциальную составляющую в ПИД регуляторе путем назначения и ни при каких значениях параметров не возникает колебаний. Кроме того, последняя формула позволяет "отключить" дифференциальную составляющую в ПИД регуляторе путем назначения 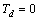 , чего нельзя сделать в выражении (5.103), поскольку при этом возникает деление на ноль. , чего нельзя сделать в выражении (5.103), поскольку при этом возникает деление на ноль.
Можно использовать еще более точные формулы численного дифференцирования и интегрирования, известные из курса численных методов решения уравнений.
Величина шага дискретизации 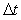 выбирается как можно меньше, это улучшает качество регулирования. Для обеспечения хорошего качества регулирования он не должен быть больше чем 1/15...1/6 от времени установления переходной характеристики объекта по уровню 0,95 или 1/4...1/6 от величины транспортной задержки [Изерман]. Однако при увеличении частоты дискретизации более чем в 2 раза по сравнению с верхней частотой спектра возмущающих сигналов (по теореме Котельникова) дальнейшего улучшения качества регулирования не происходит. выбирается как можно меньше, это улучшает качество регулирования. Для обеспечения хорошего качества регулирования он не должен быть больше чем 1/15...1/6 от времени установления переходной характеристики объекта по уровню 0,95 или 1/4...1/6 от величины транспортной задержки [Изерман]. Однако при увеличении частоты дискретизации более чем в 2 раза по сравнению с верхней частотой спектра возмущающих сигналов (по теореме Котельникова) дальнейшего улучшения качества регулирования не происходит.
Если на входе регулятора нет антиалиасного фильтра, то частоту дискретизации выбирают в 2 раза выше верхней граничной частоты спектра помехи, чтобы использовать цифровую фильтрацию. Необходимо учитывать также, что исполнительное устройство должно успеть отработать за время 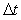 . .
Если контроллер используется не только для регулирования, но и для аварийной сигнализации, то такт дискретизации не может быть меньше, чем допустимая задержка срабатывания сигнала аварии.
При малом такте дискретизации увеличивается погрешность вычисления производной. Для ее снижения можно использовать сглаживание получаемых данных по нескольким собранным точкам перед этапом дифференцирования.
Уравнение цифрового ПИД-регулятора
Основываясь на изложенном выше, уравнение дискретного ПИД-регулятора можно записать в виде
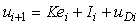 , , |
(5.106)
|
где 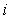 - номер временного такта. Величины - номер временного такта. Величины 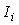 и и 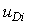 вычисляют по выражениям (5.102) и (5.105). Для начала работы алгоритма выбирают обычно вычисляют по выражениям (5.102) и (5.105). Для начала работы алгоритма выбирают обычно 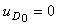 , , 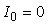 , , 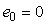 , однако могут быть и другие начальные условия, в зависимости от конкретной задачи регулирования. , однако могут быть и другие начальные условия, в зависимости от конкретной задачи регулирования.
Отметим, что алгоритм, полученный путем простой замены операторов дифференцирования и интегрирования в выражении (5.36) конечными разностями и конечными суммами
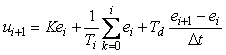 , , |
(5.107)
|
(здесь 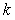 - индекс суммирования отсчетов от начала процесса до текущего i-того временного такта) обладает плохой устойчивостью и низкой точностью, как это было показано выше. Однако с ростом частоты дискретизации различие между приведенными двумя алгоритмами стирается. - индекс суммирования отсчетов от начала процесса до текущего i-того временного такта) обладает плохой устойчивостью и низкой точностью, как это было показано выше. Однако с ростом частоты дискретизации различие между приведенными двумя алгоритмами стирается.
Инкрементная форма цифрового ПИД-регулятора
|
|
|
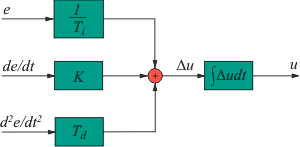
Рис. 5.83. Инкрементная форма ПИД-регулятора
|
Довольно часто, особенно в нейросетевых и фаззи-регуляторах, используют уравнение ПИД-регулятора в виде зависимости приращения управляющей величины от ошибки регулирования и ее производных (без интегрального члена). Такое представление удобно, когда роль интегратора выполняет внешнее устройство, например, обычный или шаговый двигатель. Угол поворота его оси пропорционален значению управляющего сигнала и времени. В фаззи-регуляторах при формулировке нечетких правил эксперт может сформулировать зависимость управляющей величины от величины производной, но не может - от величины интеграла, поскольку интеграл "запоминает" всю предысторию изменения ошибки, которую человек помнить не может.
Инкрементная форма ПИД-регулятора получается путем дифференцирования уравнения (5.36):
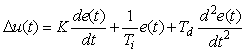 ; Для получения нулевой ошибки регулирования на выходе инкрементного регулятора должен стоять интегратор (рис. 5.83):
Переходя в полученных выражениях к конечным разностям, получим дискретную форму инкрементного ПИД-регулятора:
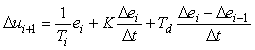 , , |
(5.108)
|
где  , , 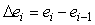 . .
Более устойчивое и точное разностное уравнение можно получить, подставив в формулу  выражения для выражения для 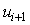 и и 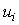 из (5.106). из (5.106).
Инкрементная форма регулятора удобна для применения в микроконтроллерах, поскольку в ней основная часть вычислений выполняется с приращениями, для представления которых можно использовать слово с малым количеством двоичных разрядов. Для получения значения управляющей величины можно выполнить накопительное суммирование на финальной стадии вычислений:
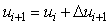 . .
|
|

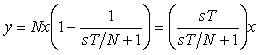 ,
,