4.3 Динамические измерения
Измеряемые физические параметры обычно изменяются с течением времени, поэтому для оценки точности измерений необходимо знать, как зависит погрешность измерений от динамических характеристик измеряемой величины, т.е. какова динамическая компонента погрешности измерений. В пользовательской документации на устройства аналогового ввода, как правило, отсутствует информация, необходимая для оценки динамической погрешности (импульсная, переходная, амплитудно-частотная и фазочастотная характеристика, амплитудно-фазовая или передаточная функция). Несмотря на то, что динамическая погрешность очень часто в несколько раз превышает статическую, ее редко принимают во внимание, поскольку измерить величину этой погрешности технически достаточно сложно и необходимые для этого приборы часто отсутствуют.
Второй проблемой, которая имеет место при вводе аналоговой информации в компьютер или контроллер, является появление алиасных (ложных) частот, которые снижают точность измерений. Опасность этого явления заключается в том, что помехи, лежащие гораздо выше частоты дискретизации, могут трансформироваться в низкочастотную область, если в измерительном канале неправильно выбран или отсутствует антиалиасный фильтр. Антиалиасный фильтр необходим для уменьшения помех на входе средства измерений, однако его наличие приводит к возникновению динамической погрешности.
Ниже описываются причины возникновения динамической погрешности и пути ее оценки.
4.3.1. Теорема Котельникова
В системах автоматизации самой распространенной операцией является дискретизация сигнала по времени. Выбор частоты дискретизации опирается на теорему Котельникова, которая распространяется на любые сигналы с ограниченным спектром. Если спектр сигнала ограничен частотой 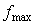 , то частота отсчетов должна быть в 2 раза выше, чтобы сигнал можно было восстановить без потери информации. Иначе говоря, если самая высокочастотная гармоника в спектре сигнала имеет период , то частота отсчетов должна быть в 2 раза выше, чтобы сигнал можно было восстановить без потери информации. Иначе говоря, если самая высокочастотная гармоника в спектре сигнала имеет период  , то на один период гармоники должно приходиться 2 отсчета при дискретизации сигнала. При этом непрерывный сигнал преобразуется в импульсный без потери информации. , то на один период гармоники должно приходиться 2 отсчета при дискретизации сигнала. При этом непрерывный сигнал преобразуется в импульсный без потери информации.
Отметим несколько особенностей применения теоремы.
Во первых, в теореме Котельникова предполагается, что сигнал 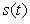 будет восстановлен с помощью замены каждого отсчета функцией будет восстановлен с помощью замены каждого отсчета функцией 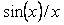 , т.е. , т.е.
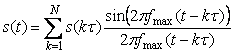 , , |
(4.61)
|
где 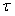 - интервал между отсчетами, - интервал между отсчетами, 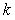 - номер отсчета, - номер отсчета, 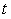 - время. Однако на практике такую функцию реализовать невозможно, поскольку ее спектральная характеристика является идеально прямоугольной и для ее получения требуется фильтр с идеально прямоугольной АЧХ. Поэтому восстановление сигнала после дискретизации выполняют с помощью фильтров невысоких порядков. - время. Однако на практике такую функцию реализовать невозможно, поскольку ее спектральная характеристика является идеально прямоугольной и для ее получения требуется фильтр с идеально прямоугольной АЧХ. Поэтому восстановление сигнала после дискретизации выполняют с помощью фильтров невысоких порядков.
Во-вторых, сигналы с ограниченным спектром имеют бесконечную протяженность во времени, а реальные сигналы, ограниченные во времени, имеют неограниченный частотный спектр, поэтому разложение их в ряд Котельникова требует пренебрежения частью спектра, лежащего выше частоты 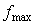 . .
В-третьих, теорема Котельникова предполагает, что при дискретизации сигнала использованы импульсы бесконечно малой длительности.
Указанные факторы являются причиной того, что на практике частоту дискретизации выбирают в несколько раз выше, чем требуется в соответствии теоремой Котельникова.
Теорема Котельникова позволяет оценить предельную пропускную способность измерительного канала с известной полосой пропускания 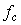 . Если средство измерений имеет погрешность . Если средство измерений имеет погрешность  , то количество различимых уровней при измерении величины , то количество различимых уровней при измерении величины 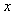 будет равно будет равно 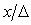 , а количество информации с мерой Хартли [Темников], полученное при однократном измерении, будет равно , а количество информации с мерой Хартли [Темников], полученное при однократном измерении, будет равно 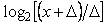 . Если систематическая составляющая погрешности исключена и преобладает случайная составляющая с дисперсией . Если систематическая составляющая погрешности исключена и преобладает случайная составляющая с дисперсией 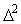 , то количество различимых уровней следует искать как отношение мощностей, т.е. количество информации будет равно , то количество различимых уровней следует искать как отношение мощностей, т.е. количество информации будет равно 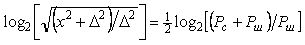 , где , где  - мощность сигнала, - мощность сигнала, 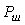 - мощность погрешности. Поскольку в соответствии с теоремой Котельникова сигнал со спектром шириной - мощность погрешности. Поскольку в соответствии с теоремой Котельникова сигнал со спектром шириной 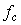 должен быть дискретизирован с частотой 2 должен быть дискретизирован с частотой 2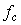 , чтобы сохранить всю содержащуюся в нем информацию, то для сигнала длительностью , чтобы сохранить всю содержащуюся в нем информацию, то для сигнала длительностью  потребуется потребуется 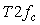 отсчетов. Следовательно, измерительный канал с полосой отсчетов. Следовательно, измерительный канал с полосой 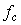 позволяет передать позволяет передать 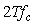 отсчетов, каждый из которых содержит отсчетов, каждый из которых содержит 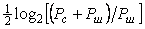 бит информации, т.е. пропускная способность канала (количество передаваемой информации в единицу времени) составит бит информации, т.е. пропускная способность канала (количество передаваемой информации в единицу времени) составит 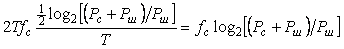 , бит/с. Величина , бит/с. Величина 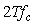 называется базой сигнала, а называется базой сигнала, а 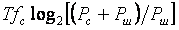 - объемом сигнала, - объемом сигнала, 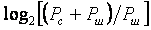 - динамическим диапазоном. - динамическим диапазоном.
4.3.2. Фильтр и динамическая погрешность
Измеряемая величина в системах автоматизации обычно не является постоянной во времени. Поэтому возникает вопрос, насколько медленно она должна изменяться, чтобы погрешность измерения не превышала заданного значения. Для ответа на этот вопрос используется понятие динамической погрешности.
Нормированию динамических погрешностей уделено недостаточно внимания как в нормативной литературе, так и в эксплуатационной документации средств измерений. Так, динамические характеристики, необходимые для оценки динамической погрешности. как правило, отсутствуют в пользовательской документации на модули аналогового ввода, за редким исключением (например, модули аналогового ввода RealLab! серии NL типа NL-8AI содержат необходимую информацию).
Оценка величины динамической погрешности является сравнительно сложным процессом. Проблема возникает потому, что динамическая погрешность зависит не только от динамической модели измерительного канала, но и от формы измеряемого сигнала.
Основными источниками динамической погрешности являются естественная инерционность физических процессов, протекающих в датчиках, процессы заряда входной емкости измерительного устройства, инерционность фильтров, использованных для устранения алиасного эффекта и подавления помех в измерительном канале.
|
|
|
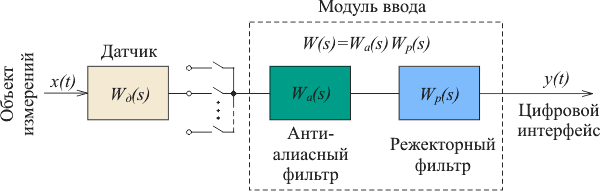
Рис. 4.9. Динамическая модель измерительного канала
|
Для количественного описания динамических свойств измерительного канала используют линейные динамические модели в виде дифференциальных уравнений, операторных передаточных функций, импульсных переходных характеристик или реакций на единичный скачок, амплитудно-частотные и амплитудно-фазовые характеристики (ГОСТ 8.256 [ГОСТ]). Описание этих моделей может быть указано в эксплуатационной документации на средство измерений. Идентификацию динамической модели средства измерений выполняет его разработчик, используя те же методы, что и при идентификации объекта управления (см. раздел "ПИД-регуляторы").
В некоторых случаях, например, когда уравнения динамической модели пользователю известны, могут быть заданы только коэффициенты уравнений, постоянные времени, время реакции (время установления), коэффициент демпфирования, полоса пропускания по уровню 0,707 и др.
Для модулей аналогового ввода может быть также задана погрешность положения отсчета измеряемого сигнала на оси времени.
Рассмотрим типовую динамическую модель измерительного канала (рис. 4.9), которая включает в себя модели датчика 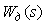 и модуля ввода аналоговых сигналов и модуля ввода аналоговых сигналов 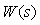 . Передаточная функция . Передаточная функция 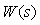 обычно представляет собой произведение передаточных функций антиалиасного фильтра (стоящего до АЦП) и цифрового режекторного фильтра после АЦП. Измерительный преобразователь часто входит в состав модуля ввода. обычно представляет собой произведение передаточных функций антиалиасного фильтра (стоящего до АЦП) и цифрового режекторного фильтра после АЦП. Измерительный преобразователь часто входит в состав модуля ввода.
При проектировании системы автоматизации динамические характеристики ее звеньев можно выбрать так, что инерционность всего измерительного канала будет определяться инерционностью самого медленного звена. Это существенно упрощает процесс оценки величины динамической погрешности. Например, при измерении температуры самым инерционным звеном должен быть датчик (инерционность термопар характеризуется постоянной времени десятки секунд и намного превышает инерционность модуля ввода (доли секунды)).
|
|
|
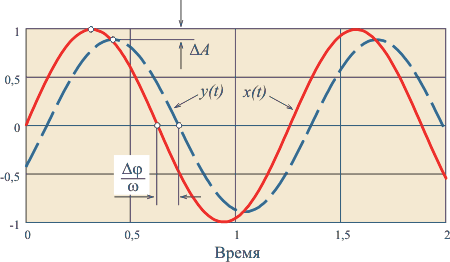
Рис. 4.10. Синусоидальный сигнал на входе 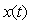 и выходе и выходе 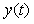 измерительного канал измерительного канал
|
Многоканальные средства измерений бывают двух типов: с коммутацией источников сигнала и с параллельно работающими каналами. В первом случае на входе модуля ввода используется аналоговый коммутатор (рис. 4.9), во втором случае коммутатор не используется, а многоканальность достигается применением нескольких одинаковых каналов с одновременно работающими АЦП.
В системе с параллельно работающими каналами можно считать, что сигнал на входе средства измерений действует неограниченно долго. При коммутации каналов сигнал объекта измерений 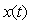 действует, пока ключ коммутатора замкнут. Описание динамической погрешности этих двух типов систем имеет свои особенности. действует, пока ключ коммутатора замкнут. Описание динамической погрешности этих двух типов систем имеет свои особенности.
Измерение при синусоидальном сигнале
Рассмотрим сначала случай, когда входной (измеряемый) сигнал изменяется по синусоидальному закону: 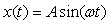 (рис. 4.10), а измерительный канал не содержит коммутатора. Считая, что канал линеен, получим на его выходе сигнал (рис. 4.10), а измерительный канал не содержит коммутатора. Считая, что канал линеен, получим на его выходе сигнал 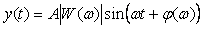 , где , где 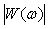 - амплитудно-частотная характеристика (АЧХ) измерительного канала, - амплитудно-частотная характеристика (АЧХ) измерительного канала, 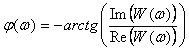 - фазо-частотная характеристика (ФЧХ)- сдвиг фазы выходного сигнала относительно входного. Таким образом, погрешность измерительного канала в данном случае состоит из двух компонент: погрешности амплитуды - фазо-частотная характеристика (ФЧХ)- сдвиг фазы выходного сигнала относительно входного. Таким образом, погрешность измерительного канала в данном случае состоит из двух компонент: погрешности амплитуды 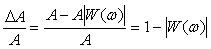
и погрешности фазы (рис. 4.10) 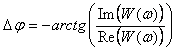 . .
Наиболее простые соотношения для оценки указанных погрешностей получаются для случая, когда динамику измерительного канала можно представить моделью первого порядка (фильтром первого порядка):
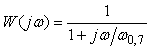 , , |
(4.64)
|
где 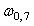 - граничная частота по уровню - граничная частота по уровню 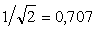 . Для нее АЧХ и ФЧХ имеют вид: . Для нее АЧХ и ФЧХ имеют вид: 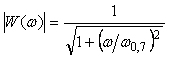 , , 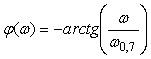 . .
Поскольку погрешность средств измерений в системах автоматизации, как правило, не превышает 1%, в приведенных соотношениях можно считать 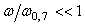 , что позволяет разложить нелинейные функции в ряд Тейлора и ограничиться первыми двумя членами разложения. При этих условиях получим , что позволяет разложить нелинейные функции в ряд Тейлора и ограничиться первыми двумя членами разложения. При этих условиях получим
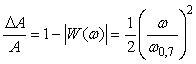 , , 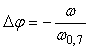 . . |
(4.65)
|
Например, если модуль ввода имеет граничную частоту 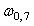 =5 Гц, то для того, чтобы динамическая погрешность не превышала 0,05%, частота входного сигнала должна составлять не более =5 Гц, то для того, чтобы динамическая погрешность не превышала 0,05%, частота входного сигнала должна составлять не более 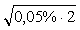 =0,032% от граничной частоты =0,032% от граничной частоты 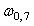 , т.е не более 0,16 Гц. , т.е не более 0,16 Гц.
Отметим, что оценки (4.65) относятся только к погрешности амплитуды и фазы синусоидального сигнала, но не к погрешности отдельных его отсчетов. Наибольшая погрешность измерения входного сигнала как функции времени будет при 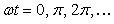 . Ее величину можно оценить следующим образом: . Ее величину можно оценить следующим образом:
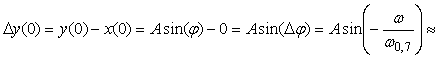 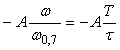 , , |
(4.66)
|
где 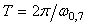 - постоянная времени фильтра, - постоянная времени фильтра, 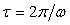 - период измеряемого сигнала. Относительная погрешность будет равна - период измеряемого сигнала. Относительная погрешность будет равна
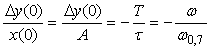 . . |
(4.67)
|
Таким образом, для получения динамической погрешности величиной 0,1% при измерении отсчетов синусоидального сигнала в моменты времени 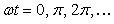 частота входного сигнала должна быть в 1000 раз ниже граничной частоты фильтра. Отметим, что погрешность амплитуды (измеренная в моменты времени частота входного сигнала должна быть в 1000 раз ниже граничной частоты фильтра. Отметим, что погрешность амплитуды (измеренная в моменты времени 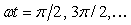 ) уменьшается в зависимости от частоты по квадратичному закону (4.65), в то время как погрешность в моменты времени ) уменьшается в зависимости от частоты по квадратичному закону (4.65), в то время как погрешность в моменты времени 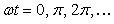 - только линейно (4.67). - только линейно (4.67).
Измерение при входном сигнале "единичный скачок"
Если входной сигнал изменяется скачком, то для измерительного канала, который описывается моделью первого порядка (4.64) и не содержит коммутатора, реакцию на скачок можно получить с помощью преобразования Лапласа. Для этого в выражении (4.64) можно вместо 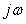 использовать комплексную частоту использовать комплексную частоту 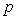 [Баскаков] и умножить (4.64) на изображение единичного скачка [Баскаков] и умножить (4.64) на изображение единичного скачка 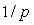 (по Лапласу). Переходя от изображения к оригиналу с помощью обратного преобразования Лапласа, получим сигнал на выходе измерительного канала как функцию времени: (по Лапласу). Переходя от изображения к оригиналу с помощью обратного преобразования Лапласа, получим сигнал на выходе измерительного канала как функцию времени:
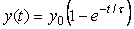 , , |
(4.68)
|
где 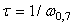 , , 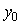 - значение - значение 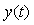 при при 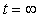 . .
Поскольку точное значение единичного скачка 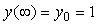 , погрешность измерений , погрешность измерений 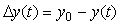 с течением времени будет уменьшаться по экспоненциальному закону: с течением времени будет уменьшаться по экспоненциальному закону:
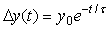 , откуда , откуда 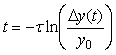 . . |
(4.69)
|
Например, для получения относительной динамической погрешности 1% измерение нужно делать не раньше чем через 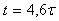 после подачи измеряемого сигнала. Для получения погрешности 0,05% задержка перед измерением должна быть не менее после подачи измеряемого сигнала. Для получения погрешности 0,05% задержка перед измерением должна быть не менее 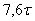 . .
Измерение сигнала произвольной формы
В случае, когда измеряемый сигнал имеет произвольную форму 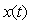 , выражение для , выражение для 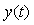 в общем случае имеет вид свертки входного сигнала и импульсной характеристики измерительного канала в общем случае имеет вид свертки входного сигнала и импульсной характеристики измерительного канала 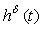 [Попов]: [Попов]:
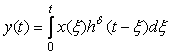 , , |
(4.70)
|
где 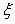 - переменная интегрирования. - переменная интегрирования.
Импульсная характеристика 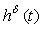 является реакцией измерительного канала на входной сигнал в форме дельта-функции Дирака является реакцией измерительного канала на входной сигнал в форме дельта-функции Дирака 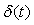 . Вместо импульсной характеристики можно использовать реакцию на единичный скачок . Вместо импульсной характеристики можно использовать реакцию на единичный скачок 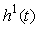 , при этом выражение для , при этом выражение для 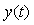 запишется в виде интеграла Дюамеля [Попов] запишется в виде интеграла Дюамеля [Попов]
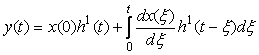 . . |
(4.71)
|
К сожалению, более простого выражения не существует и интегралы (4.70) и (4.71) нужно брать для каждой конкретной формы входного сигнала 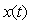 . Сделать это аналитически, как правило, невозможно. Наиболее удобным способом является численное интегрирование или моделирование, например, с помощью программ Matlab, MathCAD. . Сделать это аналитически, как правило, невозможно. Наиболее удобным способом является численное интегрирование или моделирование, например, с помощью программ Matlab, MathCAD.
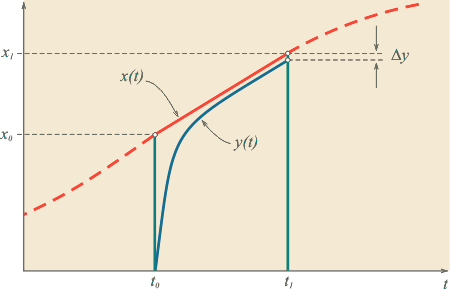
Однако для многоканальной системы сбора данных с одним АЦП и коммутацией входных каналов (рис. 4.9) получить приближенное выражение для динамической погрешности в общем случае, независимо от формы сигнала на входе системы, возможно. Для этого воспользуемся тем, что отсчеты входного сигнала в системах сбора данных берутся обычно так часто, что при разложении функции 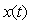 в ряд Тейлора на интервале между отсчетами можно ограничиться линейным членом разложения (4.5). Иначе говоря, при произвольной форме входного сигнала и достаточно высокой частоте дискретизации функцию в ряд Тейлора на интервале между отсчетами можно ограничиться линейным членом разложения (4.5). Иначе говоря, при произвольной форме входного сигнала и достаточно высокой частоте дискретизации функцию 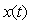 можно аппроксимировать прямой линией на участке можно аппроксимировать прямой линией на участке 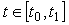 (рис. 4.124), где (рис. 4.124), где 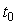 - момент замыкания ключа входного коммутатора; - момент замыкания ключа входного коммутатора; 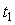 - момент появления сигнала на выходе модуля ввода: - момент появления сигнала на выходе модуля ввода:
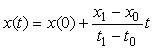 , , 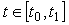 . . |
(4.72)
|
Максимальную погрешность такой аппроксимации можно оценить по величине третьего члена ряда Тейлора
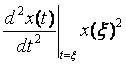 , , |
(4.73)
|
|
|
|
Рис. 4.124. Сигнал после коммутатора (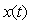 ) и на выходе модуля ввода ( ) и на выходе модуля ввода (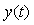 ) )
|
где точка 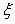 выбирается на интервале выбирается на интервале 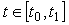 таким образом, чтобы величина второй производной в ней была наибольшей. В частности, если входной сигнал описывается линейной зависимостью, то для него таким образом, чтобы величина второй производной в ней была наибольшей. В частности, если входной сигнал описывается линейной зависимостью, то для него 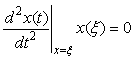 для всех точек интервала для всех точек интервала 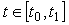 . .
Рассмотрим сначала случай с фильтром первого порядка, когда передаточная функция 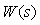 описывается выражением (4.64). Импульсную характеристику фильтра можно получить с помощью обратного преобразования Лапласа от выражения (4.64), в котором переменная описывается выражением (4.64). Импульсную характеристику фильтра можно получить с помощью обратного преобразования Лапласа от выражения (4.64), в котором переменная 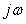 заменена на комплексную частоту заменена на комплексную частоту 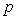 : :
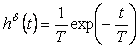 . . |
(4.74)
|
Подставляя (4.74) и (4.72) в (4.70), получим выражение для функции 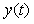 на интервале на интервале 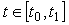 : :
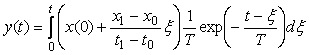 = = 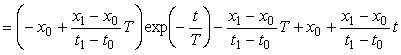 . . |
(4.75)
|
Вычитая из полученного выражения сигнал на входе 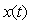 (4.72), получим величину абсолютной погрешности (4.72), получим величину абсолютной погрешности 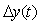 в виде в виде
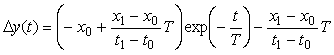 . . |
(4.76)
|
Таким образом, при достаточно большом 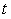 (точнее, при (точнее, при 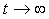 ) абсолютная динамическая погрешность не приближается к нулю, а остается постоянной, равной ) абсолютная динамическая погрешность не приближается к нулю, а остается постоянной, равной 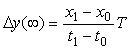 . При малых . При малых 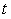 , на начальном участке переходного процесса, погрешность экспоненциально уменьшается с течением времени. , на начальном участке переходного процесса, погрешность экспоненциально уменьшается с течением времени.
Пользуясь выражением (4.76), можно записать выражение для приведенной погрешности
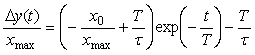 , , |
(4.77)
|
где 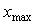 - верхняя граница диапазона измерений; - верхняя граница диапазона измерений; 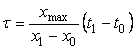 . Используя обозначение . Используя обозначение 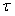 в (4.72), получим: в (4.72), получим:
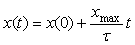 . . |
(4.78)
|
Из этой формулы виден физический смысл параметра 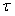 : это время, за которое входной сигнал проходит интервал от : это время, за которое входной сигнал проходит интервал от 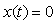 до до 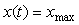 при условии, что он сохранит линейность на этом интервале. при условии, что он сохранит линейность на этом интервале.
Отметим, что при 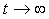 выражение (4.77) совпадает с (4.67), а при выражение (4.77) совпадает с (4.67), а при 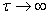 - с (4.69). - с (4.69).
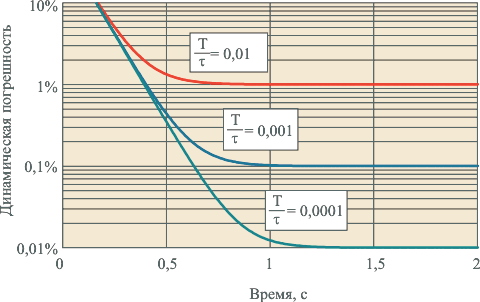
Графики зависимости модуля динамической погрешности от времени, построенные по выражению (4.77) при 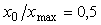 , показаны на рис. 4.125. Например, если постоянная времени фильтра первого порядка , показаны на рис. 4.125. Например, если постоянная времени фильтра первого порядка  равна 1 с, то для того, чтобы динамическая погрешность не превышала 0,1%, отношение равна 1 с, то для того, чтобы динамическая погрешность не превышала 0,1%, отношение 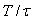 должно быть не более 0,001 (см. рис. 4.125), откуда должно быть не более 0,001 (см. рис. 4.125), откуда 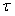 >1000 >1000 , т.е. скорость нарастания входного сигнала должна быть такой, чтобы интервал от , т.е. скорость нарастания входного сигнала должна быть такой, чтобы интервал от 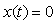 до до 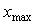 был пройден за время не менее 1000 был пройден за время не менее 1000 =1000 с. Если уравнение (4.78) нормировать на =1000 с. Если уравнение (4.78) нормировать на 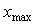 , чтобы перейти к относительным величинам , чтобы перейти к относительным величинам 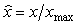 , ,
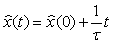 , , |
(4.79)
|
то можно сказать, что скорость нарастания входного сигнала 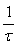 должна быть не более 0,001 должна быть не более 0,001 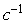 , или 0,1 , или 0,1 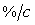 . .
Аналогичное соотношение можно получить для фильтра второго порядка с передаточной функцией 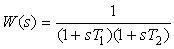 . .
Выражение для приведенной погрешности будет иметь вид
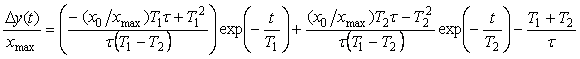 . . |
(4.80)
|
При 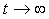 , как и в системе первого порядка, погрешность стремится к постоянной величине , как и в системе первого порядка, погрешность стремится к постоянной величине 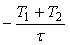 . .
Можно показать, что для фильтра 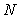 -го порядка, описываемого полиномом вида -го порядка, описываемого полиномом вида 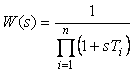 , погрешность стремится к величине , погрешность стремится к величине 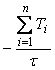 при при 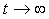 . .
Таким образом, для многоканальной системы сбора данных с одним АЦП и коммутацией входных каналов (рис. 4.9) динамическая погрешность измерений не зависит от формы измеряемого сигнала и ее величину можно оценить по графику на рис. 4.125 или формуле (4.77).
|
|
|
Рис. 4.125. Зависимость модуля динамической погрешности от времени при
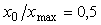 и и 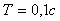 для модуля ввода с фильтром первого порядка для модуля ввода с фильтром первого порядка
|
4.3.3. Sinc-фильтр в измерительных модулях ввода
В системах автоматизации обычно используют режекторные фильтры для ослабления помехи с частотой 50 Гц, проникающей из сети питания. Такой фильтр, как правило, входит в состав микросхемы АЦП, откуда следует требование к простоте его реализации. Наиболее популярным для этих целей оказался sinc-фильтр (sinc, sinc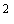 , sinc , sinc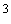 , sinc , sinc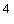 ) [Laddomada , Hogenauer]. ) [Laddomada , Hogenauer].
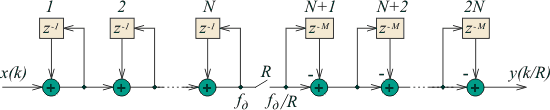
Структура цифрового sinc-фильтра представлена на рис. 4.126. Он состоит из двух каскадов: первый каскад - до ключа 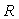 , второй - после. На вход фильтра поступают отсчеты сигнала , второй - после. На вход фильтра поступают отсчеты сигнала 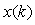 с частотой дискретизации с частотой дискретизации 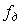 . Блок . Блок 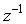 выполняет задержку на один такт отсчетов, поступающих на его вход. Блок выполняет задержку на один такт отсчетов, поступающих на его вход. Блок 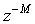 выполняет задержку на выполняет задержку на 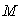 =1 или =1 или 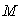 =2 тактов. Ключ =2 тактов. Ключ 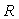 пропускает только каждый пропускает только каждый 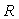 -тый отсчет, поэтому частота следования отсчетов после него и на выходе фильтра составляет -тый отсчет, поэтому частота следования отсчетов после него и на выходе фильтра составляет 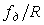 т.е. такой фильтр выполняет также функцию прореживания (децимации) отсчетов. т.е. такой фильтр выполняет также функцию прореживания (децимации) отсчетов.
|
|
|
Рис. 4.126. Структура sinc-фильтра
|
Первый каскад фильтра выполняет суммирование входных отсчетов, второй каскад выполняет функцию вычитания из поступившей на его вход суммы предыдущей суммы отсчетов (суммы, полученной на предыдущем такте 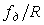 ), т.е. выбирает суммы из ), т.е. выбирает суммы из 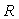 слагаемых. Таким образом, фильтр в целом выполняет операцию нахождения среднего арифметического в окне шириной слагаемых. Таким образом, фильтр в целом выполняет операцию нахождения среднего арифметического в окне шириной 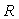 отсчетов; точнее, как будет показано ниже, в окне шириной отсчетов; точнее, как будет показано ниже, в окне шириной 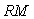 . .
Непосредственно по рис. 4.126 можно записать передаточную функцию одного звена с блоком задержки 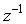 : :
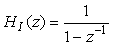 . . |
(4.81)
|
Аналогично, для одного звена с блоком 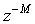 передаточная функция будет иметь вид передаточная функция будет иметь вид
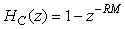 . . |
(4.82)
|
Здесь в показателе степени стоит произведение 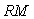 , поскольку вследствие прореживания отсчетов ключом , поскольку вследствие прореживания отсчетов ключом 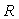 задержка отсчетов относительно задержка отсчетов относительно 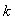 выполняется на выполняется на 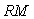 тактов. тактов.
Поскольку в фильтре использовано 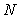 блоков до ключа и блоков до ключа и 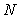 блоков после, выражение для передаточной функции всего фильтра можно записать в виде произведения блоков после, выражение для передаточной функции всего фильтра можно записать в виде произведения 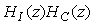 в степени в степени 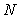 : :
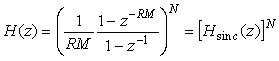 . . |
(4.83)
|
Здесь в знаменателе использован нормирующий множитель 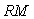 , чтобы коэффициент передачи фильтра на нулевой частоте был равен единице; , чтобы коэффициент передачи фильтра на нулевой частоте был равен единице;
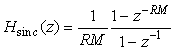 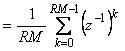 . . |
(4.84)
|
Для перехода к сумме в (4.84) использована формула суммы членов геометрической прогрессии 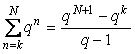 . .
Поскольку по правилам преобразования Фурье задержка оригинала на 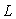 соответствует умножению изображения на соответствует умножению изображения на 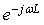 , то при частоте отсчетов , то при частоте отсчетов 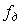 (что соответствует задержке на один такт (что соответствует задержке на один такт 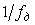 ) оператор сдвига на один такт будет равен ) оператор сдвига на один такт будет равен 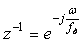 . .
Подставляя это значение в (4.84), получим Фурье-изображение передаточной функции sinc-фильтра в виде
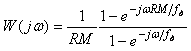 . . |
(4.85)
|
Выполнив такие же преобразования, как и в (4.53)-(4.54), получим выражение для передаточной функции sinc-фильтра в виде
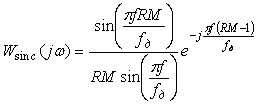 . . |
(4.86)
|
Для упрощения аналитических выкладок с sinc-фильтром его передаточную функцию упрощают путем разложения знаменателя (4.86) в ряд Тейлора с отбрасыванием всех членов, кроме первого:
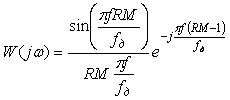 . . |
(4.87)
|
Это приближение выполняется достаточно точно, поскольку обычно частота дискретизации гораздо выше частот, на которых используется sinc-фильтр: 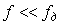 . Вероятно, такая аппроксимация объясняет название "sinc*-фильтр", хотя на самом деле функция . Вероятно, такая аппроксимация объясняет название "sinc*-фильтр", хотя на самом деле функция 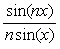 называется функцией Дирихле [Сергиенко] или периодической sinc-функцией. называется функцией Дирихле [Сергиенко] или периодической sinc-функцией.
Поскольку при 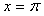 функция функция 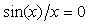 , то частота режекции фильтра находится из условия , то частота режекции фильтра находится из условия 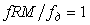 . Поэтому при типовой частоте дискретизации в АЦП . Поэтому при типовой частоте дискретизации в АЦП 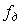 =32768 Гц для ослабления помехи c частотой =32768 Гц для ослабления помехи c частотой 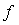 =50 Гц ( =50 Гц (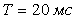 ) выбирают ) выбирают 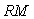 =656. =656.
Рассмотрим принцип действия фильтра во временной области. Для упрощения будем считать 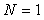 (фильтр первого порядка), т.е. с одним звеном до ключа и одним после (рис. 4.126). Звено с элементом задержки (фильтр первого порядка), т.е. с одним звеном до ключа и одним после (рис. 4.126). Звено с элементом задержки 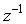 выполняет функцию интегрирования, т.е. суммирования в дискретной области. Сигнал на его выходе равен выполняет функцию интегрирования, т.е. суммирования в дискретной области. Сигнал на его выходе равен 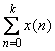 . Ключ . Ключ 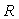 замыкается через замыкается через 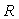 тактов и пропускает на свой выход сумму тактов и пропускает на свой выход сумму 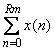 , где , где 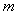 - номер прореженного отсчета (после ключа - номер прореженного отсчета (после ключа 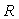 ). Звено фильтра с элементом задержки ). Звено фильтра с элементом задержки 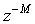 при при 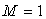 выполняет вычитание из текущей суммы отсчетов предыдущей суммы, т.е. пропускает на свой выход сумму отсчетов в окне шириной выполняет вычитание из текущей суммы отсчетов предыдущей суммы, т.е. пропускает на свой выход сумму отсчетов в окне шириной 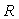 . Таким образом, sinc-фильтр первого порядка выполняет усреднение (вычисляет среднее арифметическое) входных отсчетов во временном окне шириной . Таким образом, sinc-фильтр первого порядка выполняет усреднение (вычисляет среднее арифметическое) входных отсчетов во временном окне шириной 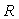 , т.е. сумму , т.е. сумму 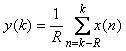 . .
Поэтому sinc-фильтр можно представить как окно, движущееся вдоль оси времени и усредняющее попадающие в него 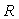 отсчетов. отсчетов.
При ширине окна, равном периоду помехи синусоидальной формы (например, помехи с частотой сети 50 Гц), среднее значение за период равно нулю. Этим объясняется подавление (режекция) sinc-фильтром помехи с частотой 50 Гц. Практически коэффициент ослабления определяется частотой отсчетов, разрядностью АЦП, погрешностью и стабильностью частоты тактового генератора фильтра. Например, ослабление sinc-фильтром помехи с частотой 50 Гц в модулях RealLab! серии NL составляет -120 дБ, см. также руководство по эксплуатации модулей серии NL (pdf 1,2 Мб).
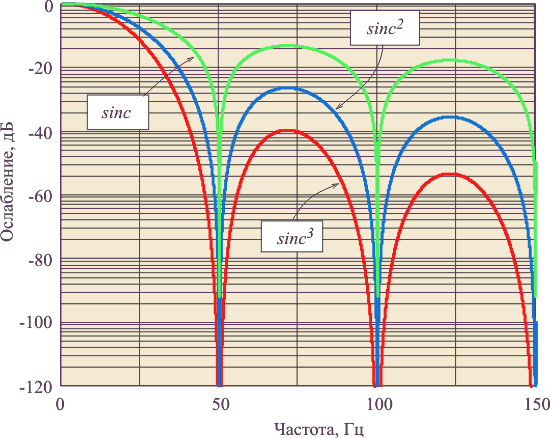
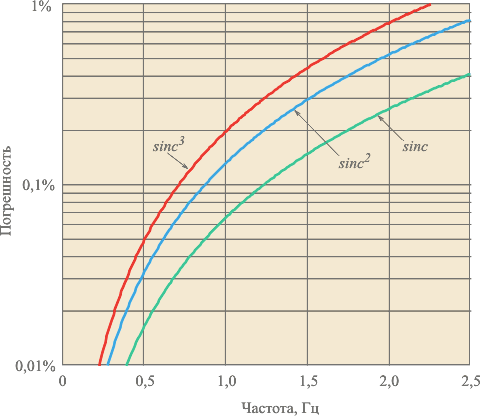
При постоянной частоте отсчетов 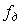 sinc-фильтр позволяет изменять частоту режекции с помощью коэффициента прореживания sinc-фильтр позволяет изменять частоту режекции с помощью коэффициента прореживания 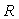 . На рис. 4.127 представлена АЧХ sinc-фильтров первого, второго и третьего порядка. Зависимость динамической погрешности измерения амплитуды синусоидального сигнала . На рис. 4.127 представлена АЧХ sinc-фильтров первого, второго и третьего порядка. Зависимость динамической погрешности измерения амплитуды синусоидального сигнала 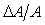 от частоты для трех sinc-фильтров с параметрами от частоты для трех sinc-фильтров с параметрами 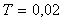 , , 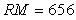 показана на рис. 4.128. показана на рис. 4.128.
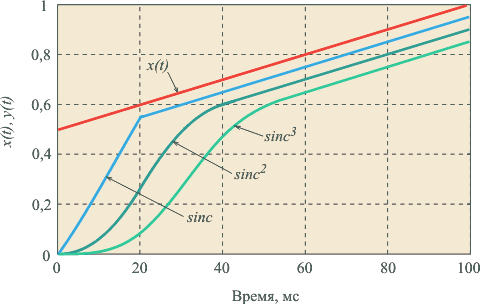
На рис. 4.129 показана реакция sinc-фильтров на линейно нарастающий сигнал (см. рис. 4.124). Как видим, линейно нарастающий сигнал проходит через фильтр с задержкой; возникающая при этом погрешность при 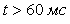 остается постоянной во времени, равной для sinc-фильтра первого порядка остается постоянной во времени, равной для sinc-фильтра первого порядка 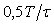 , для фильтра второго порядка - , для фильтра второго порядка - 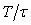 , для фильтра третьего порядка - , для фильтра третьего порядка - 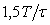 , где , где 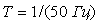 =20 мс - ширина временного окна фильтра, настроенного на частоту режекции 50 Гц. =20 мс - ширина временного окна фильтра, настроенного на частоту режекции 50 Гц.
Например, для получения динамической погрешности, равной 0,05% для sinc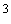 -фильтра входной сигнал должен изменяться со скоростью не более чем 100% за 60 с, или 1,67% за 1 с. Здесь проценты берутся от верхней границы динамического диапазона -фильтра входной сигнал должен изменяться со скоростью не более чем 100% за 60 с, или 1,67% за 1 с. Здесь проценты берутся от верхней границы динамического диапазона 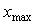 (см. (4.77)). (см. (4.77)).
4.3.4. Алиасные частоты, антиалиасные фильтры
|
а)
|
|
б)
в)
|
|
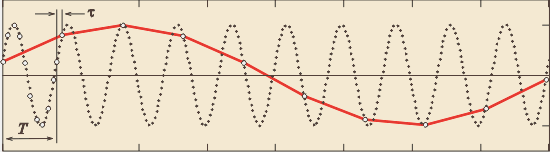
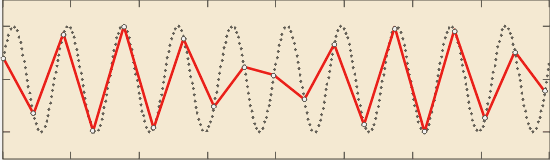
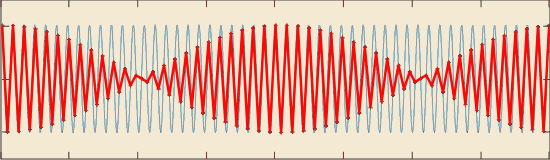
Рис. 4.130. Пояснение принципа появления алиасных частот: при 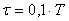 (а); (а);
при 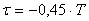 (б) и (б) и 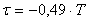 (в) (в)
|
Первой неожиданностью, с которой обычно сталкиваются те, кто первый раз начал собирать данные в компьютер, является появление низкочастотной помехи, которой нет в реальном процессе и которой, казалось бы, не должно быть в собранных данных. Помеха может иметь форму периодического сигнала (сплошная кривая на рис. 4.130-а или напоминать сигнал с амплитудной модуляцией (рис. 4.130-б, в). В реальности такой помехи нет, она появляется только после дискретизации сигнала, поэтому ее называют ложной или алиасной (от английского "alias" - "вымышленный"). Алиасные помехи увеличивают погрешность измерительных каналов.
Аналогичные эффекты проявляются и в других областях человеческой деятельности как биения колебаний, интерференция, стробоскопический эффект, муар и т. п.
Принцип образования помехи с алиасной частотой иллюстрируется рис. 4.130-а. Здесь пунктирной линией показан дискретизируемый периодический сигнал с периодом  , точки на линии показывают моменты выборки текущих значений. , точки на линии показывают моменты выборки текущих значений.
При дискретизации с высокой частотой, когда шаг дискретизации много меньше периода колебаний (таким образом дискретизирован первый период синусоидального сигнала на рис. 4.130-а), дискретизированный сигнал качественно не отличается от исходного, если пренебречь погрешностью дискретизации.
Если же шаг дискретизации приближается к периоду исходного сигнала, то, как показано сплошной линией на рис. 4.130-а, после дискретизации получается сигнал, по форме похожий на исходный, но с гораздо большим периодом. Период стремится к бесконечности при 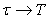 . .
|
|
|
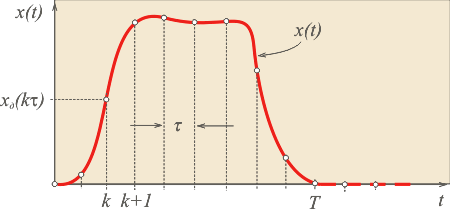
Рис. 4.131. Дискретизация непрерывного сигнала
|
Аналогичный эффект, состоящий в появлении новых компонент спектра в низкочастотной области возникает и при дискретизации функций произвольной формы. Рассмотрим этот эффект подробнее.
Пусть имеется непрерывный сигнал 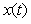 (рис. 4.131), заданный на интервале времени (рис. 4.131), заданный на интервале времени 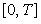 . Выберем отсчеты сигнала с шагом . Выберем отсчеты сигнала с шагом 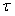 в точках в точках 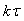 и полученную последовательность отсчетов назовем дискретным сигналом и полученную последовательность отсчетов назовем дискретным сигналом 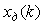 . Последовательность отсчетов можно записать в виде функции от непрерывной переменной . Последовательность отсчетов можно записать в виде функции от непрерывной переменной 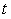 , если использовать понятие дискретной импульсной функции: , если использовать понятие дискретной импульсной функции:
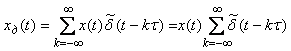 , , |
(4.88)
|
где 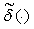 - дискретная импульсная (игольчатая) функция, определяемая как - дискретная импульсная (игольчатая) функция, определяемая как
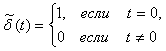 . . |
(4.89)
|
В отличие от дельта-функции Дирака, она не стремится к бесконечности при 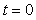 . В выражении (4.88) функция . В выражении (4.88) функция 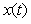 вынесена за знак суммирования потому, что она не зависит от вынесена за знак суммирования потому, что она не зависит от 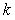 . .
Найдем спектр сигнала 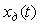 (4.88). Для этого сначала разложим функцию (4.88). Для этого сначала разложим функцию 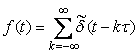 в ряд Фурье [Баскаков], воспользовавшись ее периодичностью: в ряд Фурье [Баскаков], воспользовавшись ее периодичностью:
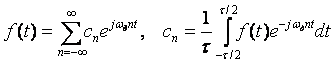 , , |
(4.90)
|
где 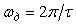 , , 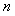 - номер коэффициента ряда, - номер коэффициента ряда, 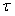 - период функции. - период функции.
Найдем коэффициенты 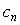 : :
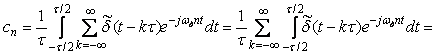 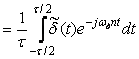 |
(4.91)
|
Знак суммирования в последнем выражении отсутствует потому, что за пределами интервала интегрирования 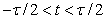 все члены суммы для все члены суммы для 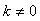 равны нулю. равны нулю.
Для того, чтобы найти интеграл (4.91), представим игольчатую функцию как предел, к которому стремится прямоугольный импульс шириной 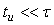 при при 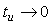 : :
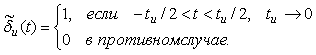 . . |
(4.92)
|
Тогда из (4.91) получим
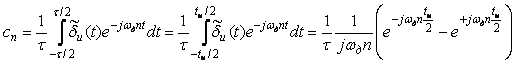 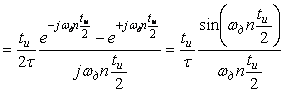 . . |
(4.93)
|
Если ширина импульса стремится к нулю, то 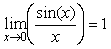 , следовательно, , следовательно,
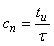 . . |
(4.94)
|
Используя это выражение, ряд Фурье для 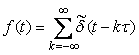 можно записать в виде (см. (4.90)): можно записать в виде (см. (4.90)):
|
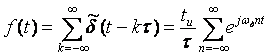 . .
|
(4.95)
|
Подставляя полученное выражение в (4.88), получим
 . . |
(4.96)
|
Здесь функция 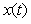 внесена под знак суммирования, поскольку она не зависит от внесена под знак суммирования, поскольку она не зависит от 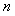 . .
Найдем теперь спектральную плотность 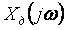 дискретного сигнала дискретного сигнала 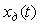 с помощью преобразования Фурье: с помощью преобразования Фурье:
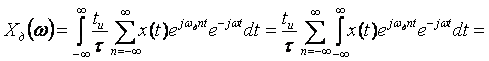 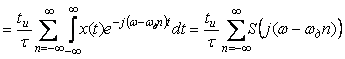 , , |
(4.97)
|
где 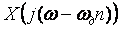 - спектральная плотность исходного непрерывного сигнала - спектральная плотность исходного непрерывного сигнала 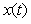 , сдвинутая по оси частот на , сдвинутая по оси частот на 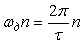 . .
Таким образом, спектр дискретного сигнала 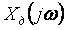 представляет собой серию копий спектров непрерывного сигнала представляет собой серию копий спектров непрерывного сигнала 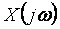 , сдвинутых друг относительно друга на частоту дискретизации , сдвинутых друг относительно друга на частоту дискретизации 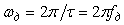 : :
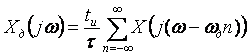 . . |
(4.98)
|
|
а)
|
|
|
б)
|
|
|
в)
|
|
|
г)
|
|
|
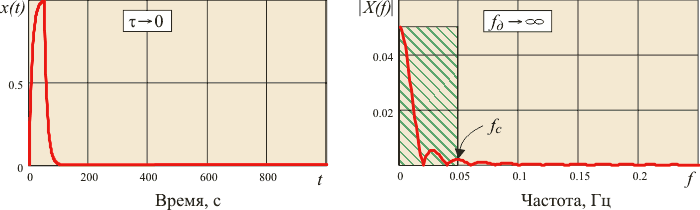
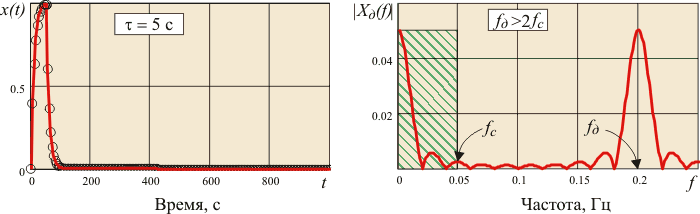
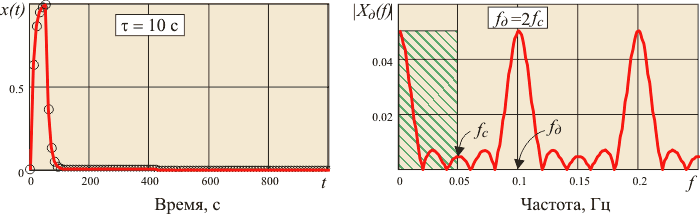
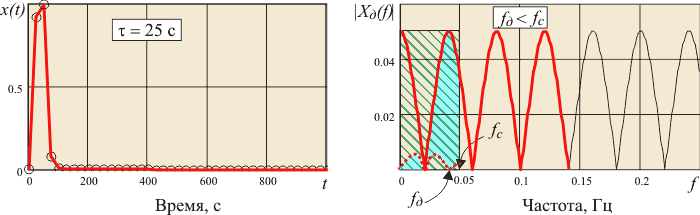
Рис. 4.132. Сигналы и их спектральные плотности: а) - непрерывный сигнал; б) - г) - дискретные сигналы. 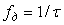 - частота дискретизации, - частота дискретизации, 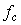 - граница спектра - граница спектра
|
На рис. 4.132-а показан график непрерывного сигнала 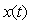 (рис. 4.132, а, слева) и модуля его спектральной плотности (рис. 4.132, а, слева) и модуля его спектральной плотности 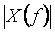 , , 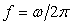 (справа). Поскольку функция (справа). Поскольку функция 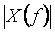 симметрична относительно оси ординат, на рис. 4.132 показан только график в правой полуплоскости. Исходный непрерывный сигнал симметрична относительно оси ординат, на рис. 4.132 показан только график в правой полуплоскости. Исходный непрерывный сигнал 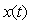 можно рассматривать как дискретный с нулевым периодом дискретизации ( можно рассматривать как дискретный с нулевым периодом дискретизации (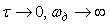 ). Поэтому модуль его спектральной плотности является непериодической функцией (рис. 4.132-а, справа). ). Поэтому модуль его спектральной плотности является непериодической функцией (рис. 4.132-а, справа).
После дискретизации функции 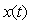 с частотой с частотой 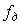 на графике модуля спектральной плотности появляется бесконечное количество копий на графике модуля спектральной плотности появляется бесконечное количество копий 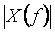 (см. рис. 4.132-б, в, справа), сдвинутых друг относительно друга на величину (см. рис. 4.132-б, в, справа), сдвинутых друг относительно друга на величину 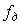 . Степень отличия спектра дискретного сигнала от спектра непрерывного характеризует величину погрешности дискретизации. С уменьшением частоты дискретизации в соответствии с (4.98) и как видно из рис. 4.132, копии спектров сближаются, увеличивая погрешность дискретизации. . Степень отличия спектра дискретного сигнала от спектра непрерывного характеризует величину погрешности дискретизации. С уменьшением частоты дискретизации в соответствии с (4.98) и как видно из рис. 4.132, копии спектров сближаются, увеличивая погрешность дискретизации.
Предположим, что вся полезная информация, содержащаяся в непрерывном сигнале, заключена в области от 0 до частоты 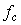 , которую поэтому можно считать границей спектра непрерывного сигнала (на рис. 4.132 эта область спектра заштрихована). Если для восстановления сигнала используется фильтр с граничной частотой , которую поэтому можно считать границей спектра непрерывного сигнала (на рис. 4.132 эта область спектра заштрихована). Если для восстановления сигнала используется фильтр с граничной частотой 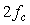 (см. рис. 4.132-в), который убирает все составляющие спектра, лежащие выше (см. рис. 4.132-в), который убирает все составляющие спектра, лежащие выше 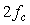 , то наличие копий в спектре дискретного сигнала не искажает форму сигнала после его восстановления. , то наличие копий в спектре дискретного сигнала не искажает форму сигнала после его восстановления.
Если же ближайшая копия спектра приблизится к оригиналу настолько, что внесет искажения в его форму, (см. рис. 4.132-г), то восстановить исходный сигнал становится невозможно. Поэтому для исключения наложения спектров частота дискретизации 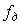 должна быть по крайней мере в 2 раза выше граничной частоты спектра должна быть по крайней мере в 2 раза выше граничной частоты спектра 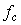 , т.е. , т.е. 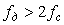 , как и требуется по теореме Котельникова. , как и требуется по теореме Котельникова.
Спектр произвольного непрерывного сигнала, показанный на рис. 4.132-а, в общем случае является неограниченным. Поэтому копии спектров, появляющиеся после дискретизации, всегда частично перекрываются. Это является причиной потери информации при восстановлении сигнала. И только для сигнала с ограниченным спектром эффект наложения отсутствует, что позволяет восстановить сигнал без потери информации.
Описанный алиасный эффект не может быть устранен с помощью цифровой фильтрации, если частота дискретизации равна удвоенной частоте верхней границы спектра полезного сигнала, т. к. при этом в спектре дискретизированного сигнала будет потеряна информация о помехах. Для решения этой проблемы можно использовать аналоговый (антиалиасный) фильтр с граничной частотой 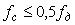 на входе блока дискретизации или выбрать частоту дискретизации выше верхней граничной частоты спектра помех, чтобы в последующем выполнить цифровую фильтрацию. на входе блока дискретизации или выбрать частоту дискретизации выше верхней граничной частоты спектра помех, чтобы в последующем выполнить цифровую фильтрацию.
В модулях аналогового ввода антиалиасный фильтр обычно настроен на максимальную частоту дискретизации, обеспечиваемую модулем и не может быть перестроен. Поэтому, если при измерении медленно протекающих процессов частота дискретизации программно выбрана низкой, а антиалиасный фильтр не перестроен, то помеха не ослабляется антиалиасным фильтром и поэтому в измеренном сигнале появляются алиасные помехи.
|


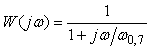 ,
,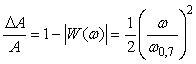 ,
, 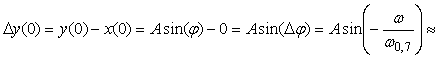
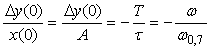 .
.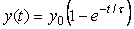 ,
,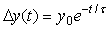 , откуда
, откуда 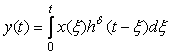 ,
,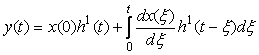 .
.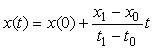 ,
, 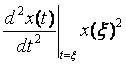 ,
,
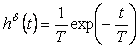 .
.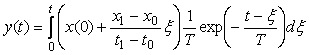 =
= 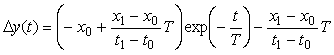 .
.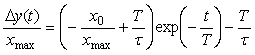 ,
,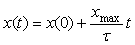 .
.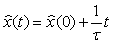 ,
,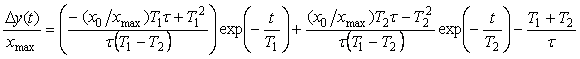 .
.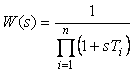 , погрешность стремится к величине
, погрешность стремится к величине 

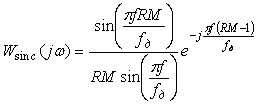 .
.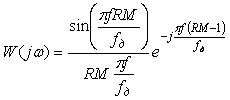 .
.




 ,
,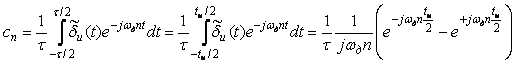
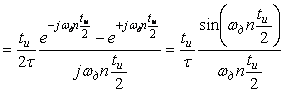 .
.










